题目内容
17.△ABC内接于⊙O,过点O作OH⊥BC于点H,延长OH交⊙O于点D,连接AD.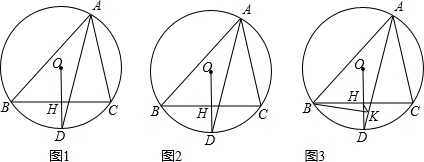
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,若OH=DH,求∠BAC的度数;
(3)如图3,在(2)的条件下,过点B作BK⊥AD于点K,连接HK,若HK=$\frac{3}{2}$,⊙O的半径为$\frac{7\sqrt{3}}{3}$,求AC的长.
分析 (1)由OH⊥BC知$\widehat{BD}=\widehat{CD}$,可得∠BAD=∠CAD;
(2)RT△BOH中由OH=$\frac{1}{2}$OB知∠BOH=60°,进而得∠BAC=$\frac{1}{2}$∠BOC=60°;
(3)延长BK、AC交于点P,连接OB,过点C作CR⊥AB,在RT△BOH中根据半径及∠BOH求得BH、BC的长,证△ABK≌△APK得BK=PK、AB=AP,结合BH=CH可得CP=2HK=3,设AC=m,则AB=m+3,在RT△ACR中表示出CR、AR的长,在RT△BCR中根据勾股定理可求得m的值,即AC的长.
解答 解:(1)∵OH⊥BC于点H,
∴$\widehat{BD}=\widehat{CD}$,
∴∠BAD=∠CAD;
(2)如图2,连接OB、OC,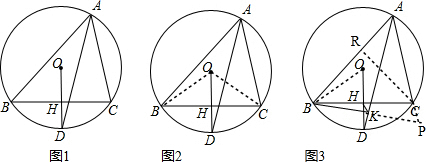 ∵OH=DH,OB=OD,
∵OH=DH,OB=OD,
∴OH=$\frac{1}{2}$OB,而OH⊥BH,
∴∠OBH=30°,∠BOH=60°
∴∠BAC=$\frac{1}{2}$∠BOC=60°;
(3)如图3,延长BK、AC交于点P,连接OB,过点C作CR⊥AB于点R,
在RT△BOH中,OB=$\frac{7\sqrt{3}}{3}$,∠BOH=60°,
∴BH=OB•sin60°=$\frac{7}{2}$,
∵OH⊥BC,
∴BH=CH,
∴BC=2BH=7,
∵BK⊥AD,
∴∠AKB=∠AKP=90°,
在△ABK和△APK中,
$\left\{\begin{array}{l}{∠BAK=∠PAK}\\{AK=AK}\\{∠AKB=∠AKP}\end{array}\right.$,
∴△ABK≌△APK(ASA),
∴BK=PK,AB=AP,
∵BH=CH,
∴HK是△BCP的中位线,
∴CP=2HK=3,
设AC=m,则AB=AP=m+3,
在RT△ACR中,∠RAC=60°,
∴AR=$\frac{1}{2}$m,CR=$\frac{\sqrt{3}}{2}$m,
∴BR=AB-AR=m+3-$\frac{1}{2}$m=$\frac{1}{2}$m+3,
在RT△BCR中,BR2+CR2=BC2,即($\frac{1}{2}$m+3)2+($\frac{\sqrt{3}}{2}$m)2=72,
解得:m=5或m=-8(舍),
∴AC=5.
点评 此题考查了圆周角定理、垂径定理、全等三角形的判定等知识.该题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

 阅读快车系列答案
阅读快车系列答案
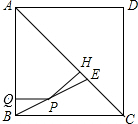 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
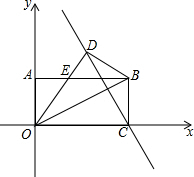 如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.
如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.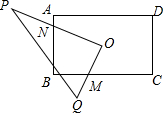 如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$.
如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$.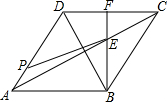 已知菱形ABCD边长为5cm,tan∠DAB=$\frac{4}{3}$,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F.若点P为AD上一点,且∠DPE+∠DAB=90°,则AP长为$\frac{5}{3}$.
已知菱形ABCD边长为5cm,tan∠DAB=$\frac{4}{3}$,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F.若点P为AD上一点,且∠DPE+∠DAB=90°,则AP长为$\frac{5}{3}$.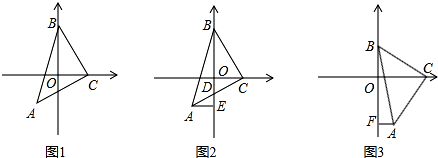
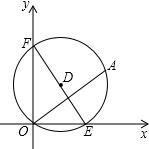 如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两坐标轴的正半轴交于点E、F.当EF⊥OA时,此时EF=$\frac{125}{24}$.
如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两坐标轴的正半轴交于点E、F.当EF⊥OA时,此时EF=$\frac{125}{24}$.