题目内容
7.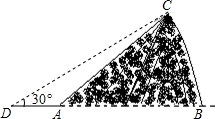 如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
分析 首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形△DEC、△AEC,应利用其公共边EC构造等量关系,借助DE=AE+DA构造方程关系式,进而可求出答案.
解答 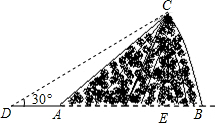 解:作CE⊥DB于点E,
解:作CE⊥DB于点E,
由山坡AC的坡度为i=1:1,设山高EC=x米,则AE=x米,
由tan30°=$\frac{EC}{DE}$,得$\frac{{\sqrt{3}}}{3}=\frac{x}{300+x}$,
解得$x=\frac{{300\sqrt{3}}}{{3-\sqrt{3}}}$≈409米.
答:山的高度约为409米.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,由山坡AC的坡度得出CE和AE的关系,再由三角函数求出AE,继而求出CE.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
15.现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如表:
(1)求这两种货车各多少辆?
(2)如果各安排9辆货车前往甲、乙两地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为W元,求出W与a的函数关系式.(写出自变量取值范围)
| 运往地 车型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 700 | 600 |
| 小货车 | 500 | 450 |
(2)如果各安排9辆货车前往甲、乙两地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为W元,求出W与a的函数关系式.(写出自变量取值范围)
16.某企业招聘员工,要求所要应聘者都要经过笔试与面试两种考核,且按考核总成绩从高到低进行录取,如果考核总成绩相同时,则优先录取面试成绩高分者.下面是招聘考和总成绩的计算说明:
笔试总成绩=(笔试总成绩+加分)÷2
考和总成绩=笔试总成绩+面试总成绩
现有甲、乙两名应聘者,他们的成绩情况如下:
(1)甲、乙两人面试的平均成绩为85.35,;
(2)甲应聘者的考核总成绩为145.6;
(3)根据上表的数据,若只应聘1人,则应录取甲.
笔试总成绩=(笔试总成绩+加分)÷2
考和总成绩=笔试总成绩+面试总成绩
现有甲、乙两名应聘者,他们的成绩情况如下:
| 应聘者 | 成绩 | ||
| 笔试成绩 | 加分 | 面试成绩 | |
| 甲 | 117 | 3 | 85.6 |
| 乙 | 121 | 0 | 85.1 |
(2)甲应聘者的考核总成绩为145.6;
(3)根据上表的数据,若只应聘1人,则应录取甲.
16.对于圆的周长公式C=2πR,下列说法错误的是( )
| A. | π是变量 | B. | R、C是变量 | C. | R是自变量 | D. | C是因变量 |
17.某企业为了增收节支,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,根据所描出的点猜想y是x的什么函数,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)为了支持希望工程,在实际的销售过程中该公司决定每销售一件工艺品就捐a(a<4)元给希望工程,公司通过销售记录发现,当销售单元价不超过51/件时,每天扣除捐赠后的日销售利润随销售单价x的增大而增大,求a的取值范围.
| 销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)为了支持希望工程,在实际的销售过程中该公司决定每销售一件工艺品就捐a(a<4)元给希望工程,公司通过销售记录发现,当销售单元价不超过51/件时,每天扣除捐赠后的日销售利润随销售单价x的增大而增大,求a的取值范围.
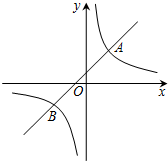 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.