题目内容
12.在函数y=$\frac{k}{x}$(k≠0)的图象上有三点(-1,y1),(-2,y2),(3,y3),如果y2<y1,则y2和y3的大小关系为y2>y3.分析 由0>x1>x2,得到y2<y1,于是得到k<0,函数y=$\frac{k}{x}$(k≠0)的图象在二,四象限,得到点(3,y3)在第四象限,y3<0,于是得到结论.
解答 解:∵x1=-1,x2=-2,
∴0>x1>x2,
∵y2<y1,
∴k<0,
∴函数y=$\frac{k}{x}$(k≠0)的图象在二,四象限,
∵x3=3>0,
∴点(3,y3)在第四象限,
∴y3<0,
∴y2>y3.
故答案为:y2>y3.
点评 本题考查了反比例函数图象上点的坐标特征,熟练掌握点的坐标特征是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.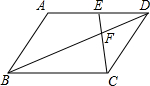 在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
 在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
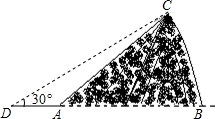 如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).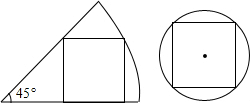 一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为1,则扇形纸板和圆形纸板的面积比是5:4.
一张圆心角为45°的扇形纸板和圆形纸板按如图方式剪得一个正方形,边长都为1,则扇形纸板和圆形纸板的面积比是5:4.