题目内容
4．已知一个平行四边形的两条对角线长分别是12和18，则此平行四边形四边中点连接所成的新四边形的周长是30．分析 如图，首先证明MN、PQ分别为△ABD、△ACD的中位线，求出MN、PQ的长度；同理求出MQ、PN的长度，即可解决问题．
解答 
解：如图，在平行四边形ABDC中，
∵M、N、P、Q分别为四边的中点，
∴MN、PQ分别为△ABD、△ACD的中位线，
∴MN=PQ=$\frac{1}{2}AD$=9；同理可求MQ=PN=$\frac{1}{2}BC$=6，
∴新四边形的周长=2×9+2×6=30．
点评 该题主要考查了中点四边形的性质、三角形的中位线定理等几何知识点及其应用问题；牢固掌握三角形的中位线定理等几何知识点是基础，灵活运用、解题是关键．
练习册系列答案
相关题目
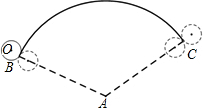如图，若弧BC的半径AB为12，圆心角为120°，半径为2的⊙O，从弧BC的一个端点B（切点）开始沿弧滚动到另一个端点C（切点），则⊙O需要转动2周．
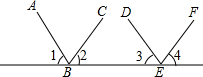完成下列推理说明：