题目内容
12. 如图,矩形OABC中,OA=4,OC=8,点D是线段OB的中点,点P从点A出发,以每秒1个单位的速度沿射线AO作匀速运动,点Q从点O出发,以每秒2个单位的速度沿x轴正半轴作匀速运动,P,Q同时出发,设运动的时间为t.
如图,矩形OABC中,OA=4,OC=8,点D是线段OB的中点,点P从点A出发,以每秒1个单位的速度沿射线AO作匀速运动,点Q从点O出发,以每秒2个单位的速度沿x轴正半轴作匀速运动,P,Q同时出发,设运动的时间为t.(1)求点B,点D的坐标;
(2)函数y=$\frac{k}{x}$经过点D,R为y=$\frac{k}{x}$上一点,在P,Q的整个运动过程中,若以点P,Q,B,R为顶点的四边形是平行四边形,求R点的坐标.
分析 (1)由矩形的对边相等得出点B(8,4),由中点定义得D(4,2);
(2)分两种情形①如图1中,当P在线段OA上时,四边形PQRB是平行四边形,如图2中,当点P在AO的延长线上时,四边形PQBR是平行四边形,利用全等三角形的性质,列出方程即可解决问题.
解答 解:(1)∵四边形OABC是矩形,
∴BC=OA=4,
∵OC=8,
∴B(8,4),
∵点D是线段OB的中点,
∴D(4,2);
(2)∵函数y=$\frac{k}{x}$经过点D,
∴k=4×2=8,
∴y=$\frac{8}{x}$,
如图1中,当P在线段OA上时,四边形PQRB是平行四边形,作RM⊥BC于M,
由△POQ≌△BMR,得BM=OP,RM=OQ,
∴R(8+t,$\frac{8}{8+t}$),
∵OP=BM,
∴4-t=4-$\frac{8}{8+t}$,
∴t2+8t-8=0,解得t=-4+2$\sqrt{3}$或-4-2$\sqrt{3}$(舍弃).
如图2中,当点P在AO的延长线上时,四边形PQBR是平行四边形,作RM⊥BC于M.
由△POQ≌△BMR得到,OP=BM,OQ=RM,
∴点R($\frac{8}{8-t}$,8-t),
∵OQ=RM,
∴t=8-$\frac{8}{8-t}$,
∴t2-16t+56=0,
∴t=8±$\sqrt{13}$,
∴t=-4+2$\sqrt{3}$或8±$\sqrt{13}$秒时,P,Q,B,R为顶点的四边形是平行四边形.
点评 本题考查反比例函数、平行四边形、矩形的性质、全等三角形的性质等知识,解题的关键是灵活应用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
7.若点A(2,-2),B(-1,-2),则直线AB与x轴和y轴的位置关系分别是( )
| A. | 平行,垂直相交 | B. | 平行,平行 | C. | 相交、相交 | D. | 垂直相交,平行 |
 如图,AB∥EM∥DC,AE=ED,EF∥BC,EF=12cm,则BC的长为24cm.
如图,AB∥EM∥DC,AE=ED,EF∥BC,EF=12cm,则BC的长为24cm.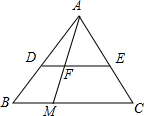 如图,已知△ABC,DE∥BC,交AB于点D,交AC于点E,点M在边BC上,AM交DE于点F.
如图,已知△ABC,DE∥BC,交AB于点D,交AC于点E,点M在边BC上,AM交DE于点F. 两个形状相同、大小相等的小木块放置于桌面上,其俯视图如图,则其主视图是( )
两个形状相同、大小相等的小木块放置于桌面上,其俯视图如图,则其主视图是( )


