题目内容
10.二次函数y=ax2-2ax+a-2的图象与y轴交于点C,与x轴交于点A、B两点,O为坐标原点,若OC2=OA•OB,则a=1或1+$\sqrt{2}$.分析 设A(m,0),B(n,0),利用二次函数的性质和判别式的意义得到a≠0,△=4a2-4a(a-2)>0,则a>0,利用根与系数的关系得到mn=$\frac{a-2}{a}$,所以OA•OB=|mn|=|$\frac{a-2}{a}$|=$\frac{|a-2|}{a}$,再确定C(0,a-2),所以(a-2)2=$\frac{|a-2|}{a}$,然后讨论:当0<a<2时,(a-2)2=-$\frac{a-2}{a}$,当a>2时,(a-2)2=$\frac{a-2}{a}$,再分别解方程确定满足条件的a的值.
解答 解:设A(m,0),B(n,0),
根据题意得a≠0,
△=4a2-4a(a-2)>0,解得a>0,
∵mn=$\frac{a-2}{a}$,
∴OA•OB=|mn|=|$\frac{a-2}{a}$|=$\frac{|a-2|}{a}$,
当x=0时,y=a-2,则C(0,a-2),
∵OC2=OA•OB,
∴(a-2)2=$\frac{|a-2|}{a}$,
当0<a<2时,(a-2)2=-$\frac{a-2}{a}$,整理得a2-2a+1=0,解得a1=a2=1,
当a>2时,(a-2)2=$\frac{a-2}{a}$,整理得a2-2a-1=0,解得a1=1+$\sqrt{2}$,a2=1-$\sqrt{2}$(舍去),
综上所述,a的值为1或1+$\sqrt{2}$.
故答案为1或1+$\sqrt{2}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程;△=b2-4ac决定抛物线与x轴的交点个数.

练习册系列答案
相关题目
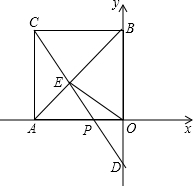 在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D.
在平面直角坐标系xOy中,四边形OACB是正方形,A点的坐标为(-3,0),点P是射线AO上(异于点A、O)一动点,直线CP与对角线AB及y轴分别交于点E,D. 为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度.
为测量塔的高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是45°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是40m,根据以上观测数据,求观光塔CD的高度. 如图,已知点D是线段AB上的一点,延长线段AB至C,使得AB=BC,且DC=5AD,若BD=4cm,求线段AC的长.
如图,已知点D是线段AB上的一点,延长线段AB至C,使得AB=BC,且DC=5AD,若BD=4cm,求线段AC的长.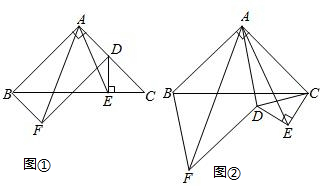
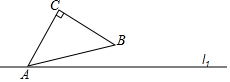 点c是直线l1外一定点,点A是直线l1上一动点,以AC为腰作等腰直角三角形ABC(点B在点C的右侧),当点A在直线l1上运动时,请画出点B的轨迹.
点c是直线l1外一定点,点A是直线l1上一动点,以AC为腰作等腰直角三角形ABC(点B在点C的右侧),当点A在直线l1上运动时,请画出点B的轨迹. 如图,在四边形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四边形ABCD.
如图,在四边形ABCD中,∠D=90°,AB=12,CD=3,DA=4,BC=13,求S四边形ABCD. 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{FC}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.