题目内容
11．
如图，在△ABC中，∠ABC和∠ACB的平分线交于点F，过点F作EG∥BC分别交AB、AC于点E、G，若BE+CG=18，则线段EG的长为（ ）| A． | 16 | B． | 17 | C． | 18 | D． | 19 |
分析 利用角平分线和平行可证得∠EBD=∠EDB，∠GDC=∠GCD，可得到DE=BE，DG=GC，可得到EG=BE+GC．
解答 解：∵EG∥BC，
∴∠EDB=∠DBC，
∵BD平分∠ABC，
∴∠EBD=∠DBC，
∴∠EBD=∠EDB，
∴ED=BE，
同理DG=GC，
∴EG=ED+DG=BE+GC=18．
故选C．
点评 本题主要考查等腰三角形的判定和性质，掌握等角对等边是解题的关键，注意平行线的性质的应用．
练习册系列答案
相关题目
2．
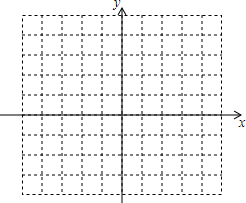在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为2：1，把三角形EFO缩小，则点E的对应点E′的坐标是（ ）
在平面直角坐标系中，已知点E（-4，2），F（-2，-2），以原点O为位似中心，相似比为2：1，把三角形EFO缩小，则点E的对应点E′的坐标是（ ）| A． | （-2，1） | B． | （-8，4） | C． | （-8，4）或（8，-4） | D． | （-2，1）或（2，-1） |
19．
如图，△ABC中，AB=AC，∠BAC=120°，D是BC中点，DE⊥AB于点E，则BE是AE的（ ）
如图，△ABC中，AB=AC，∠BAC=120°，D是BC中点，DE⊥AB于点E，则BE是AE的（ ）| A． | 1倍 | B． | 2倍 | C． | 3倍 | D． | 4倍 |
6．
如图：在△ABC中，MN∥BC，若BM=4AM，MN=1，则BC的长是（ ）
如图：在△ABC中，MN∥BC，若BM=4AM，MN=1，则BC的长是（ ）| A． | 6 | B． | 5 | C． | 4 | D． | 3 |
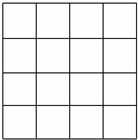如图，正方形网格中的每个小正方形边长都是1，请在图中画出△ABC使得A、B、C三点都在小正方形的顶点且AB=AC=$\sqrt{5}$，BC=$\sqrt{2}$，并求出所画三角形的面积．
20．
在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证等式（ ）
在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证等式（ ）| A． | （a+b）2=a2+2ab+b2 | B． | （a-b）2=a2-2ab+b2 | ||
| C． | a2-b2=（a+b）（a-b） | D． | （a+b）（a-2b）=a2-ab-2b2 |
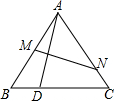如图，点M、N分别是等边三角形ABC中AB，AC边上的点，点A关于MN的对称点落在BC边上的点D处．若$\frac{BD}{DC}$=$\frac{2}{3}$，则$\frac{AM}{AN}$的值$\frac{7}{8}$．