题目内容
1.如果方程kx2+4x+3=0有两个不相等的实数根,那么k的值满足k<$\frac{4}{3}$且k≠0.分析 根据一元二次方程的定义和判别式的意义得到k≠0且△=42-4k•3>0,然后求出两不等式的公共部分即可.
解答 解:根据题意得k≠0且△=42-4k•3>0,
所以k<$\frac{4}{3}$且k≠0.
故答案为k<$\frac{4}{3}$且k≠0.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.不要漏掉二次项系数k≠0.

练习册系列答案
相关题目
11.下列命题中,
①正五边形是中心对称图形;
②在同圆或等圆中,相等的弧所对的圆周角相等;
③三角形有且只有一个外接圆;
④平分弦的直径垂直于弦,并且平分弦所对的两条弧.
其中是真命题的有( )
①正五边形是中心对称图形;
②在同圆或等圆中,相等的弧所对的圆周角相等;
③三角形有且只有一个外接圆;
④平分弦的直径垂直于弦,并且平分弦所对的两条弧.
其中是真命题的有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.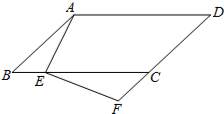 如图,在?ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.求证:BE•EC=FC•CD.
如图,在?ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.求证:BE•EC=FC•CD.



 如图,在△ABC中,∠ABC和∠ACB的平分线交于点F,过点F作EG∥BC分别交AB、AC于点E、G,若BE+CG=18,则线段EG的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点F,过点F作EG∥BC分别交AB、AC于点E、G,若BE+CG=18,则线段EG的长为( )