题目内容
 热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为300
热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为300| 3 |
| 2 |
| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:计算题
分析:在直角三角形AOM中,由AO与∠M的度数求出OM的长,在直角三角形AON中,由AO的长与∠ANO的度数求出ON的长,由OM-ON即可求出MN的长.
解答:解:在Rt△AOM中,∠M=30°,AO=300
米,
∴tanM=
,即OM=
=900米,
在Rt△AON中,∠ANO=45°,AO=300
米,
∴tan∠ANO=
,即ON=
=300
米,
则MN=OM-ON=900-300
≈380(米).
| 3 |
∴tanM=
| AO |
| OM |
300
| ||||
|
在Rt△AON中,∠ANO=45°,AO=300
| 3 |
∴tan∠ANO=
| AO |
| ON |
300
| ||
| 1 |
| 3 |
则MN=OM-ON=900-300
| 3 |
点评:此题考查了解直角三角形的应用-仰角俯角问题,弄清题中的数据是解本题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列数中,绝对值最大的是( )
A、
| ||
| B、0 | ||
| C、-2 | ||
| D、-1 |
 如图,过y轴上点A的一次函数y=ax+b与反比例函数y=
如图,过y轴上点A的一次函数y=ax+b与反比例函数y=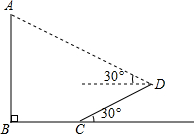 已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知
已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知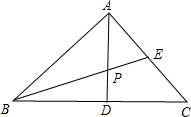 如图,已知△ABC中,∠A=90°,AD是BC边上的高,BE是角平分线,且交AD于P.
如图,已知△ABC中,∠A=90°,AD是BC边上的高,BE是角平分线,且交AD于P.