题目内容
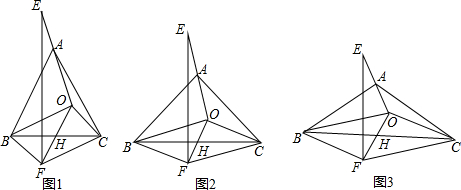
13.如图1,已知△ABC中,∠C=90°,AC=6,BC=8,点E,F在AC,BC上,将△ABC沿EF折叠,点C落在点D处,设△EDF与四边形ABFE重叠部分面积为y,CF长为x.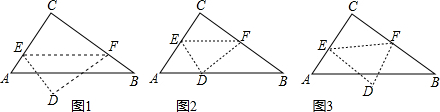
(1)如图2,当EF∥AB,CF=4时,试求y的值;
(2)当EF∥AB时,试求y与x的函数关系式,并求x为何值时y的值最大;
(3)如图3,当CF=4,DF⊥BC时,求y的值.
分析 (1)根据直角三角形的面积求出CD=4.8,由CF=BF=4,且EF∥AB,求出CH=DH即可;
(2)分两段,①用相似表示出线段CN=0.6x,EF=$\frac{5}{4}$x,用面积公式计算,②用相似表示出∵DH=CH=0.6x,DM=1.2x-4.8,EF,GI再用面积公式计算即可;
(3)先计算出△CEF的面积,再求出△DMN的面积,即可.
解答 解:(1)如图1,连接CD,
∵CF=4,BC=8,
∴BF=4,CD=$\frac{AC×BC}{AB}$=4.8,
∵EF∥AB,
∴EF=$\frac{1}{2}$AB=5,CH=DH=$\frac{1}{2}$CM=2.4,
∴y=$\frac{1}{2}$×EF×DH=$\frac{1}{2}$×5×2.4=6;
(2)①当0<x≤4时,如图2,作CM⊥AB,则CM必过点D,
由(1)有CM=4.8
∵EF∥AB,
∴$\frac{CN}{CM}=\frac{CF}{BC}$=$\frac{EF}{AB}$,
∴$\frac{CN}{4.8}=\frac{x}{8}$=$\frac{EF}{10}$,
∴CN=0.6x,EF=$\frac{5}{4}$x
∴y=S△DEF=S△CEF=$\frac{1}{2}$×EF×CN=$\frac{1}{2}$×$\frac{5}{4}$x×0.6x=$\frac{3}{8}$x2,
∴当x=4时,ymax=$\frac{3}{8}$×42=6;
②当4<x≤8,如图3,
作CM⊥AB,FN⊥AB,
∴$\frac{BF}{CF}=\frac{FN}{CM}$,
∵CF=x,
∴BF=8-x,
由(1)有,CM=4.8,
∴$\frac{8-x}{8}=\frac{FN}{4.8}$,
∴FN=0.6(8-x),
∵DH=CH=CM-MN=CM-FN=4.8-0.6(8-x)=0.6x,
DM=DH-MH=CH-FN=0.6x-0.6(8-x)=1.2x-4.8
∵EF∥AB,
∴$\frac{EF}{AB}=\frac{CH}{CM}$,∴$\frac{EF}{10}=\frac{0.6x}{4.8}$
∴EF=$\frac{5}{4}$x,
∵EF∥AB,
∴$\frac{DM}{DH}=\frac{GI}{EF}$,
∴$\frac{1.2x-4.8}{0.6x}$=$\frac{GI}{\frac{5}{4}x}$
∴GI=$\frac{5}{2}$(x-4),
∴y=$\frac{1}{2}$(GI+EF)×FN=$\frac{1}{2}$×[$\frac{5}{2}$(x-4)+$\frac{5}{4}$x]×0.6(8-x)=-$\frac{9}{8}$(x-$\frac{16}{3}$)2+8,
∴当x=$\frac{16}{3}$时,ymax=$\frac{64}{5}$.
即:x=$\frac{16}{3}$时,ymax=$\frac{64}{5}$.
(3)如图4,在CB上取一点H使CH=DM,作∠CHG=∠DMN,
在Rt△ABC中,AC=6,BC=8,∴tan∠B=$\frac{AC}{BC}$=$\frac{6}{8}$=$\frac{3}{4}$,
在△BFM中,DF⊥BC,BF=BC-CF=4,∠B+∠BMF=90°,∴tan∠B=$\frac{FM}{BF}$=$\frac{FM}{4}$=$\frac{3}{4}$,∴FM=3,∴CH=DM=1,
∵∠CHG=∠DMN,∠BMF=∠DMN,∴∠CHG=∠BMF,∵∠B+∠BMF=90°,∵∠B+∠CHG=90°,∵∠CHG+∠CGH=90°,∴∠B=∠CGH,
在Rt△HCG中,tan∠CGH=$\frac{CH}{CG}$=tan∠B=$\frac{3}{4}$,∴CG=$\frac{4}{3}$×CG=$\frac{4}{3}$,
,∵∠BFD=90°,
由折叠有∠CFE=∠DFE=45°,∴CE=CF
∴y=S四边形EFMN=S△DEF-S△DMN=S△CEF-S△CHG=$\frac{1}{2}$CE×CF-$\frac{1}{2}$×CH×CG=$\frac{1}{2}$×4×4-$\frac{1}{2}$×1×$\frac{4}{3}$=$\frac{22}{3}$.
点评 此题是几何变换综合题,主要考查了锐角三角函数,相似三角形的性质和判定,三角形,四边形面积计算公式,解本题的关键是用相似表示相关的线段,作出辅助线是解本题的难点.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 无法确定 |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
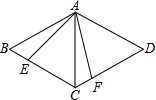 如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F.
如图,AC是菱形ABCD的对角线,∠B=60°,以点A为顶点作∠EAF=60°,∠EAF的两边分别交BC,CD于点E,F.