题目内容
19.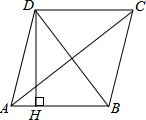 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,试求DH的长.
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,试求DH的长.
分析 根据菱形的面积等于对角线积的一半,可求得菱形的面积,又由菱形的对角线互相平分且垂直,可根据勾股定理得AB的长,根据菱形的面积的求解方法:底乘以高或对角线积的一半,即可得菱形的高.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=4,OB=OD=3,
∴AB=5cm,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=AB•DH,
∴DH=$\frac{AC•BD}{2AB}$=4.8.
点评 此题考查了菱形的性质:菱形的对角线互相平分且垂直;菱形的面积的求解方法:底乘以高或对角线积的一半.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
9.根据下列条件,能判定△ABC≌△DEF的是( )
| A. | AB=DE,BC=EF,∠A=∠D | B. | ∠A=∠D,∠C=∠F,AC=DF | ||
| C. | ∠B=∠E,∠A=∠D,AC=EF | D. | AB=DE,BC=EF,∠B=∠D |
10.下列图形中,由AB∥CD,能使∠1=∠2成立的是( )
| A. |  | B. |  | C. |  | D. |  |
4. 如图,有一块直角三角形纸片,两直角边分别为:AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,有一块直角三角形纸片,两直角边分别为:AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
 如图,有一块直角三角形纸片,两直角边分别为:AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,有一块直角三角形纸片,两直角边分别为:AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 2 cm | B. | 3 cm | C. | 4 cm | D. | 5 cm |
11.下列计算中,正确的是( )
| A. | (xn)3n=x4n | B. | (x2)3+(x3)2=2x6 | C. | (a3)n+1=a3n+1 | D. | (-a2)4•a8=-a16 |
