题目内容
6．
如图，四边形ABCD内接于⊙O，∠A=110°，则∠BOD的度数是（ ）| A． | 70° | B． | 110° | C． | 120° | D． | 140° |
分析 依据圆内接四边形的性质求得∠C的度数，然后再求得∠BOD的度数即可．
解答 解：∵四边形ABCD内接于⊙O，
∴∠A+∠C=180°．
∴∠C═180°-110°=70°．
∴∠BOD=2∠C=140°．
故选：D．
点评 本题主要考查的是圆内接四边形的性质、圆周角定理的应用，求得∠C的度数是解题的关键．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
12．如果分式$\frac{3}{x-1}$有意义，则x的取值范围是（ ）
| A． | 全体实数 | B． | x≠1 | C． | x=1 | D． | x＞1 |
13．
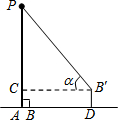小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（ ）
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（ ）| A． | $\frac{1}{1-sinα}$ | B． | $\frac{1}{1+sinα}$ | C． | $\frac{1}{1-cosα}$ | D． | $\frac{1}{1+cosα}$ |
14．下列各组中的两个图形，不一定相似的是（ ）
| A． | 有一个角是120°的两个等腰三角形 | B． | 两个等边三角形 | ||
| C． | 两个直角三角形 | D． | 两个等腰直角三角形 |
1．
如图，⊙O的圆心角∠BOC=112°，点D在弦BA的延长线上且AD=AC，则∠D的度数为（ ）
如图，⊙O的圆心角∠BOC=112°，点D在弦BA的延长线上且AD=AC，则∠D的度数为（ ）| A． | 28° | B． | 56° | C． | 30° | D． | 41° |
某农场拟建三间长方形种牛饲养室，饲养室的一面靠墙（墙长50m），中间用两道墙隔开（如图）．已知计划中的建筑材料可建墙的总长度为48m，则这三间长方形种牛饲养室的总占地面积的最大值为144m2．
如图，大海中某灯塔P周围10海里范围内有暗礁，一艘海轮在点A处观察灯塔P在北偏东60°方向，该海轮向正东方向航行8海里到达点B处，这时观察灯塔P恰好在北偏东45°方向．如果海轮继续向正东方向航行，会有触礁的危险吗？试说明理由．（参考数据：$\sqrt{3}$≈1.73）