题目内容
3.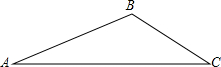 如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,
如图,△ABC,AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,(1)此三角形绕着AC旋转一周,请你描述所得的几何体,并求出上述几何体的表面积;
(2)一只蚂蚁要从B点出发绕上述几何体爬一圈回到原地,求蚂蚁爬过的最短路线长.
分析 (1)分别计算两个圆锥的侧面积后相加即可得到结果.
(2)首先求得展开扇形的圆心角的度数,然后分两种情况得到两种结果即可比较出最短线路的长.
解答  解:(1)是一个分别以AB和BC为母线,且两个底面重合的圆锥组合在一起的几何体
解:(1)是一个分别以AB和BC为母线,且两个底面重合的圆锥组合在一起的几何体
过B点作BD⊥AC于点D,
∵AB=18,sinA=$\frac{1}{6}$,sinC=$\frac{1}{3}$,
∴BD=3,
∴BC=9,
∴S=π×3×18+π×3×9=81π;
(2)∵S1=$\frac{{n}_{1}{πR}_{1}^{2}}{360}$,
∴n1=$\frac{360{S}_{1}}{{πR}_{1}^{2}}$=$\frac{360×27π}{π×{9}^{2}}$=120°,
连接BB′,过点C作BB′的垂线,垂足为E,
则由垂径定理可知BE=B′E,
∴BB′=2BE=2BC×sin60°=2×9×$\frac{\sqrt{3}}{2}$=9$\sqrt{3}$.
如左边,同理可得另一最短路线为18.
∵9$\sqrt{3}$<9×$\sqrt{4}$=9×2=18,
∴蚂蚁爬过的最短路线长为9$\sqrt{3}$
∵18>$9\sqrt{3}$
∴d=$9\sqrt{3}$.
点评 本题考查的是平面展开-最短路径问题,根据题意画出圆锥的侧面展开图是解答此题的关键.

练习册系列答案
相关题目
11.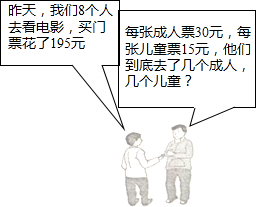 如图,设他们中有x个成人,y个儿童根据图中的对话可得方程组( )
如图,设他们中有x个成人,y个儿童根据图中的对话可得方程组( )
 如图,设他们中有x个成人,y个儿童根据图中的对话可得方程组( )
如图,设他们中有x个成人,y个儿童根据图中的对话可得方程组( )| A. | $\left\{\begin{array}{l}{x+y=30}\\{30x+15y=195}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=195}\\{30x+15y=8}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=8}\\{30x+15y=195}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=15}\\{30x+15y=195}\end{array}\right.$ |
18. 下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
(1)李刚6次成绩的极差是10分;中位数是90分.
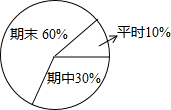
(2)如果用如图的权重给李刚打分,他应该得多少分?
 下表是李刚一学期数学成绩记录,根据信息回答下面的问题:
下表是李刚一学期数学成绩记录,根据信息回答下面的问题:| 考试类别 | 平时 | 期中考试 | 期末考试 | |||
| 第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
| 成绩 | 88 | 86 | 90 | 92 | 90 | 96 |
(2)如果用如图的权重给李刚打分,他应该得多少分?
 如图是l0×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.
如图是l0×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上.