题目内容
 如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为
如图,矩形ABCD中,AD=4,CD=1,以AD为直径作半圆O,则阴影部分面积为考点:扇形面积的计算,含30度角的直角三角形,矩形的性质,垂径定理
专题:
分析:过点O作OE⊥BC于点E,连接OF,OG,由垂径定理可知GF=2EG,根据直角三角形的性质可知∠EGO=30°,求出EG的长,再根据S阴影=S半圆-S弓形GF=S半圆-S扇形+S△GOF.
解答: 解:过点O作OE⊥BC于点E,连接OF,OG,由垂径定理可知GF=2EG,
解:过点O作OE⊥BC于点E,连接OF,OG,由垂径定理可知GF=2EG,
∵OE=CD=1,OG=
AD=2,
∴∠EGO=30°,EG=
=
=
,
∴∠EOG=60°,GF=2EG=2
,
∴∠GOF=120°,
∴S阴影=S半圆-S弓形GF=S半圆-S扇形+S△GOF=
π•22-
+
×2
×1=
+
.
故答案为:
+
.
 解:过点O作OE⊥BC于点E,连接OF,OG,由垂径定理可知GF=2EG,
解:过点O作OE⊥BC于点E,连接OF,OG,由垂径定理可知GF=2EG,∵OE=CD=1,OG=
| 1 |
| 2 |
∴∠EGO=30°,EG=
| OG2-OE2 |
| 22-12 |
| 3 |
∴∠EOG=60°,GF=2EG=2
| 3 |
∴∠GOF=120°,
∴S阴影=S半圆-S弓形GF=S半圆-S扇形+S△GOF=
| 1 |
| 2 |
| 120π•22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 2π |
| 3 |
| 3 |
故答案为:
| 2π |
| 3 |
| 3 |
点评:本题考查的是扇形面积的计算,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
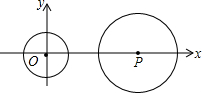 如图,平面直角坐标系中,⊙O半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,与⊙P与⊙O相切时,a的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,与⊙P与⊙O相切时,a的值为( )| A、3 | B、1 | C、1,3 | D、±1,3 |
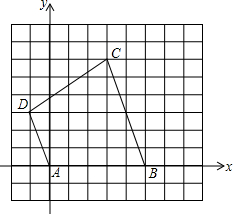 如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.
如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.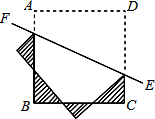 如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为
如图,已知正方形ABCD的边长为2,将正方形ABCD沿直线EF折叠,则图中折成的4个阴影三角形的周长之和为 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: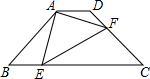 如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4
如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=4