题目内容
19.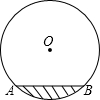 在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )| A. | 6m | B. | 8m | C. | 10m | D. | 12m |
分析 如图,油面AB上升1分米得到油面CD,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理得AE=$\frac{1}{2}$AB=3m,CF=$\frac{1}{2}$CD=4m,设OE=xm,则OF=(x-1)m,在Rt△OAE中和Rt△OCF中,根据勾股定理求得OA、OC的长度,然后由OA=OC,列方程求x即可求半径OA,得出直径MN.
解答  解:如图,依题意得AB=6m,CD=8m,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
解:如图,依题意得AB=6m,CD=8m,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
由垂径定理,得AE=$\frac{1}{2}$AB=3m,CF=$\frac{1}{2}$CD=4m,设OE=xm,则OF=(x-1)m,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x-1)2,
解得x=4,
∴半径OA=$\sqrt{{3}^{2}+{4}^{2}}$=5(m),
∴直径MN=2OA=10m.
故选:C.
点评 本题考查了垂径定理的运用.关键是利用垂径定理得出两个直角三角形,根据勾股定理表示半径的平方,根据半径相等列方程求解.

练习册系列答案
相关题目
10.用下列各图表示数轴,正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
11.已知P1(x1,y1)、P2(x2,y2)、P3(x3,y3)是反比例函数y=$\frac{10}{x}$的图象上的三点,且x1<x2<0<x3,则y1、2、y3的大小关系是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
8. 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
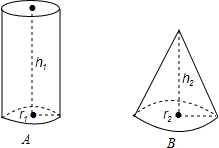 如图所示,已知B的底面周长比A大2πcm,r1:r2=2:3,VA比VB多$\frac{2}{3}$,h1+h2=18cm.问:
如图所示,已知B的底面周长比A大2πcm,r1:r2=2:3,VA比VB多$\frac{2}{3}$,h1+h2=18cm.问: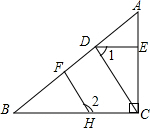 如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1+∠2=180°.求证:HF⊥AB.
如图,已知AC⊥BC,CD⊥AB,DE⊥AC,∠1+∠2=180°.求证:HF⊥AB.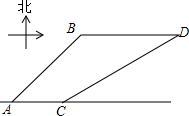 如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?
如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?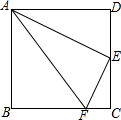 如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.
如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.