题目内容
16.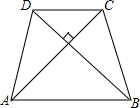 如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.
如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.(1)按要求画图,并标注字母:作CE∥BD,交AB的延长线于点E,作CF⊥AB于点F.
(2)求证:△ADC≌△CBE;
(3)求梯形的高.
分析 (1)根据题意画出图形即可;
(2)先根据四边形DCEB是平行四边形得出CD=BE,DB=CE,再由SSS定理即可得出结论;
(3)根据AC⊥BD,CE∥BD得出AC⊥CE,故△ACE是等腰直角三角形.再根据CF⊥AE可知CF=$\frac{1}{2}$AE.故S△ACE=S△ACB+S△CBE=S梯形ABCD=100,由此可得出结论.
解答 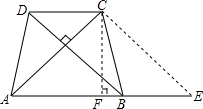 (1)解:如图所示;
(1)解:如图所示;
(2)证明:∵CE∥BD,CD∥BE,
∴四边形DCEB是平行四边形,
∴CD=BE,DB=CE.
∵AC=BD,
∴AD=CE.
在△ADC与△CBE中,
$\left\{\begin{array}{l}AD=BC\\ CD=BE\\ AC=CE\end{array}\right.$,
∴△ADC≌△CBE(SSS);
(3)解:∵AC⊥BD,CE∥BD,
∴AC⊥CE,
∴△ACE是等腰直角三角形.
∵CF⊥AE,
∴CF=$\frac{1}{2}$AE.
∵S△ACE=S△ACB+S△CBE=S梯形ABCD=100,
∴S△ACE=$\frac{1}{2}$AE•CF=CF2=100,
∴CF=10.
点评 本题考查的是等腰梯形的性质,熟知等腰梯形的两腰相等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.圆中与半径相等的弦所对的圆周角度数是( )
| A. | 30° | B. | 60° | C. | 150° | D. | 30°或 150° |
11.已知P1(x1,y1)、P2(x2,y2)、P3(x3,y3)是反比例函数y=$\frac{10}{x}$的图象上的三点,且x1<x2<0<x3,则y1、2、y3的大小关系是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
8. 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
 如图,已知点A在平面直角坐标系的位置,其坐标可能是( )
如图,已知点A在平面直角坐标系的位置,其坐标可能是( )| A. | (3,4) | B. | (-3,4) | C. | (3,-4) | D. | (-3,-4) |
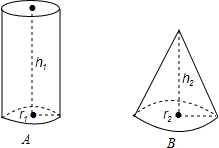 如图所示,已知B的底面周长比A大2πcm,r1:r2=2:3,VA比VB多$\frac{2}{3}$,h1+h2=18cm.问:
如图所示,已知B的底面周长比A大2πcm,r1:r2=2:3,VA比VB多$\frac{2}{3}$,h1+h2=18cm.问: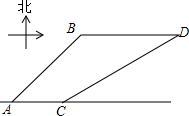 如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?
如图,港口B在港口A的东北方向,相距40$\sqrt{2}$海里,上午9时,一艘轮船从港口A出发,以15海里/时的速度向正东方向航行,同时一艘快艇从港口B出发也向正东方向航行,上午11时轮船到达C处,同时快艇到达D处,测试测得D在C的北偏东60°方向上,求快艇每小时航行多少海里?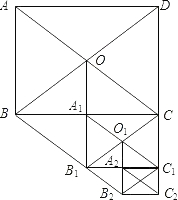 如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.
如图,在矩形ABCD中,AB=6,BC=10,两条对角线相交于点O,以OB,OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积是$\frac{15}{16}$.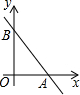 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,点P(m,0)为x轴上一点.