题目内容
 如图,矩形ABCD中,AB=4,AD=6,以为A圆心,R长为半径作圆,⊙A仅与直线BC、CD中一条相离,R的取值范围是
如图,矩形ABCD中,AB=4,AD=6,以为A圆心,R长为半径作圆,⊙A仅与直线BC、CD中一条相离,R的取值范围是考点:直线与圆的位置关系
专题:
分析:根据与两条直线中的一条相离确定与两条直线的具体的位置关系,然后确定R的取值范围即可.
解答:解:∵以为A圆心,R长为半径的⊙A仅与直线BC、CD中一条相离,
∴应该与BC相切或相交,与CD相离,
∴R的取值范围是4≤R<6.
故答案为:4≤R<6.
∴应该与BC相切或相交,与CD相离,
∴R的取值范围是4≤R<6.
故答案为:4≤R<6.
点评:本题考查了直线与圆的位置关系,解题的关键是了解相交、相切和相离与圆的半径的大小关系,难度不大.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 已知:二次函数y=ax2+bx+c列说法中正确的是( )
已知:二次函数y=ax2+bx+c列说法中正确的是( )| A、a+b+c>0 |
| B、ab>0 |
| C、b+2a=0 |
| D、当y>0,-1<x<3 |
已知二次函数y=ax2+bx+c图象开口向上,与x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
| A、abc<0 |
| B、b=2a |
| C、a+b+c=0 |
| D、2a+b=0 |
 如图,AB是⊙O的直径,∠ABC=45°,AC=AB,BC交⊙O于点D.
如图,AB是⊙O的直径,∠ABC=45°,AC=AB,BC交⊙O于点D.
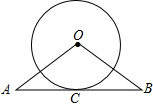 如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长.
如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长. 如图,已知△ABC中,点D、E分别在边AB、AC上,DE∥BC,若AD=4,BD=2,DE=3,那么BC=
如图,已知△ABC中,点D、E分别在边AB、AC上,DE∥BC,若AD=4,BD=2,DE=3,那么BC= 如图,在下列条件中,能证明△ABD≌△ACD的是
如图,在下列条件中,能证明△ABD≌△ACD的是