题目内容
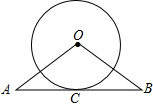 如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长.
如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16,求OA的长.考点:切线的性质,勾股定理
专题:计算题
分析:连接OC,根据等腰三角形三线合一的性质可求得AC的长,然后在直角△OAC中,利用勾股定理即可求得OA的长.
解答:解:连结OC,
∵C为切点,
∴OC⊥AB,即OC是△OAB的高,
∵∠A=∠B,
∴OA=OB,即△OAB是等腰三角形,
∴AC=CB=
AB=
×16=8,
在Rt△OCA,OA=
=
=10.
∵C为切点,
∴OC⊥AB,即OC是△OAB的高,
∵∠A=∠B,
∴OA=OB,即△OAB是等腰三角形,
∴AC=CB=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OCA,OA=
| AC2+OC2 |
| 82+62 |
点评:本题主要考查圆的切线性质及勾股定理,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决问题.

练习册系列答案
相关题目
下列图形中,( )不是多面体.


| A、(2)(4)(5) |
| B、(1)(2)(4) |
| C、(2)(5)(6) |
| D、(1)(3)(6) |
一个正多边形的外角与它相邻的内角之比为1:4,那么这个多边形的边数为( )
| A、8 | B、9 | C、10 | D、12 |
下列说法正确的有( )
①任意一个三角形都有且只有一个外接圆;
②任意一个圆都有且只有一个外切三角形;
③三角形的外心到三角形三个顶点的距离相等;
④三角形的内心可能在三角形内部也可能在三角形外部;
⑤三角形任意两边垂直平分线的交点是三角形的外心;
⑥若三角形的外心与内心重合,则这个三角形一定是等边三角形.
①任意一个三角形都有且只有一个外接圆;
②任意一个圆都有且只有一个外切三角形;
③三角形的外心到三角形三个顶点的距离相等;
④三角形的内心可能在三角形内部也可能在三角形外部;
⑤三角形任意两边垂直平分线的交点是三角形的外心;
⑥若三角形的外心与内心重合,则这个三角形一定是等边三角形.
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图的几何体,从左面看到的是( )
如图的几何体,从左面看到的是( )A、 |
B、 |
C、 |
D、 |
 已知,Rt△ABC中,AC=BC=24,⊙O和边BC相切于点D.
已知,Rt△ABC中,AC=BC=24,⊙O和边BC相切于点D. 如图,在△ABC中,点D在边AC上,AE分别交线段BD、边BC于点F、G,∠1=∠2,
如图,在△ABC中,点D在边AC上,AE分别交线段BD、边BC于点F、G,∠1=∠2, 如图,矩形ABCD中,AB=4,AD=6,以为A圆心,R长为半径作圆,⊙A仅与直线BC、CD中一条相离,R的取值范围是
如图,矩形ABCD中,AB=4,AD=6,以为A圆心,R长为半径作圆,⊙A仅与直线BC、CD中一条相离,R的取值范围是