题目内容
9.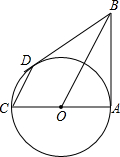 如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.
如图,AB与⊙O相切于点A,AC为⊙O的直径,且AC=6,CD∥BO,CD交⊙O于D,连接BD.(1)求证:BD与⊙O相切;
(2)若BO+CD=11,求AB的长.
分析 (1)欲证明BD与⊙O相切,只要证明∠BDO=∠BAO=90°,可以通过证明△BOA≌△BOD即可证明.
(2)连接AD,设CD=a,BO=b,想办法列出方程组,最后在RT△AOB中利用勾股定理解决.
解答 (1)证明:连接OD.
∵AB是⊙O切线,
∴∠BAO=90°,
∵CD∥OB,
∴∠AOB=∠C,∠ODC=∠BOD,
∵OD=OC,
∴∠C=∠ODC,
∴∠BOA=∠BOD,
在△BOD和△BOA中,
$\left\{\begin{array}{l}{BO=BO}\\{∠BOA=∠BOD}\\{OA=OD}\end{array}\right.$,
∴△BOA≌△BOD,
∴∠BDO=∠BAO=90°,
∴OD⊥BD,
∴BD是⊙O的切线.
(2)连接AD,设CD=a,BO=b,
∵AC是直径,
∴∠ADC=∠BA0=90°,
∵∠AOB=∠C,
∴△OAB∽△CDA,
∴$\frac{OA}{CD}$=$\frac{OB}{AC}$,
∴$\frac{3}{a}$=$\frac{b}{6}$,
∴ab=18,又a+b=11,
∴a=2,b=9或a=9,b=2(舍弃),
∴CD=2,OB=9,
在RT△AOB中,∵∠OAB=90°,OB=9,OA=3,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\sqrt{{9}^{2}-{3}^{2}}$=6$\sqrt{2}$.
点评 本题考查切线的判定和性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会转化的思想,把问题转化为方程组解决,属于中考常考题型.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.下表记录了小敏等四名学生五次数学测验成绩的平均数与方差:
根据表中数据,要从中挑选一名成绩好又比较稳定的同学参加我区的数学头脑运动会,你认为应该选( )
| 衡量指标 | 小敏 | 小芳 | 小聪 | 小明 |
| 平均数 | 90 | 85 | 90 | 85 |
| 方差 | 3 | 3 | 10 | 12 |
| A. | 小明 | B. | 小芳 | C. | 小聪 | D. | 小敏 |
 如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.
如图,在?ABCD中,连接BD,BD⊥BC,CD=4,sinC=$\frac{3}{4}$,则?ABCD的面积是3$\sqrt{7}$.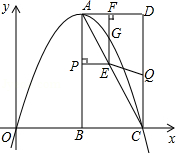 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E.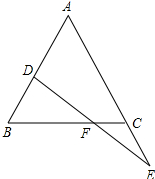 已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.
已知如图,点D在AB上,点E在AC的延长线上,且BD=CE,FD=FE.求证:△ABC是等腰三角形.