题目内容
8.已知二次函数y=x2+bx+c的图象经过点(-1,0),(4,0),则c=-4.分析 由于已知抛物线与x轴的交点坐标,则可用交点式表示解析式为y=(x+1)(x-4),然后变形为一般式即可得到c的值.
解答 解:抛物线的解析式为y=(x+1)(x-4),即y=x2-3x-4,
所以c=-4.
故答案为-4.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
19.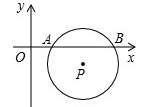 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )
 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
3.若式子|x|=(x-1)0成立,则x的取值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 不存在 |
17.如图中,∠1与∠2是对顶角的是( )
| A. |  | B. | 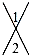 | C. | 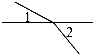 | D. | 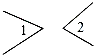 |
 如图,将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置,旋转角为a (0°<a<90°).若∠1=110°,则a=20°.
如图,将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置,旋转角为a (0°<a<90°).若∠1=110°,则a=20°. 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为24cm2,求△BEF的面积.
如图,D是△ABC的边BC上任意一点,E、F分别是线段AD、CE的中点,且△ABC的面积为24cm2,求△BEF的面积.