题目内容
19.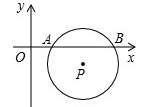 如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=$2\sqrt{3}$.将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切( )| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
分析 作PC⊥AB于点C,由垂径定理即可求得AC的长,根据勾股定理即可求得PA的长,再分点P向上平移与向下平移两种情况进行讨论即可.
解答  解:连接PA,作PC⊥AB于点C,由垂径定理得:
解:连接PA,作PC⊥AB于点C,由垂径定理得:
AC=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{3}$=$\sqrt{3}$,
在直角△PAC中,由勾股定理得:PA2=PC2+AC2,即PA2=12+($\sqrt{3}$)2=4,
∴PA=2,
∴○P的半径是2.
将○P向上平移,当○P与x轴相切时,平移的距离=1+2=3;
将○P向下平移,当○P与x轴相切时,平移的距离=2-1=1.
故选D.
点评 本题考查的是直线与圆的位置关系,通过垂径定理把求线段的长的问题转化为解直角三角形的问题是关键.

练习册系列答案
相关题目
9.下面哪个式子的计算结果是9-x2( )
| A. | (3-x)(3+x) | B. | (x-3)(x+3) | C. | (3-x)2 | D. | (3+x)2 |
10.下列调查中适合采用普查的是( )
| A. | 调查市场上某种牛奶中蛋白质的含量 | |
| B. | 调查鞋厂生产的鞋底能承受的弯折次数 | |
| C. | 了解某班学生感染流感病毒的人数 | |
| D. | 了解我市“十三”规划知晓的情况 |
7.抛物线y=-5x2-x+9与y轴的交点坐标为( )
| A. | (9,0) | B. | (-9,0) | C. | (0,-9) | D. | (0,9) |
4.$\sqrt{100}$的结果是( )
| A. | ±10 | B. | $\sqrt{10}$ | C. | -10 | D. | 10 |