题目内容
若一个多边形的内角和等于1080°,则这个多边形的边数是( )
| A、9 | B、8 | C、7 | D、6 |
考点:多边形内角与外角
专题:
分析:多边形的内角和可以表示成(n-2)•180°,依此列方程可求解.
解答:解:设所求正n边形边数为n,
则1080°=(n-2)•180°,
解得n=8.
故选:B.
则1080°=(n-2)•180°,
解得n=8.
故选:B.
点评:本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.

练习册系列答案
相关题目
 如图,∠BCA=90°,CD⊥AB,则图中互余的角有( )对.
如图,∠BCA=90°,CD⊥AB,则图中互余的角有( )对.| A、1 | B、2 | C、3 | D、4 |
下列运算正确的是( )
A、
| ||
| B、|-3|=-3 | ||
| C、(-2)3=-8 | ||
| D、-32=9 |
下列各组中,两个单项式是同类项的是( )
| A、3a2b,3a2c | ||||
| B、2a,a2 | ||||
C、
| ||||
| D、-5,8 |
下列说法正确的是( )
| A、弦是直径 |
| B、长度相等的弧是等弧 |
| C、圆的切线垂直于半径 |
| D、90°的圆周角所对的弦是直径 |
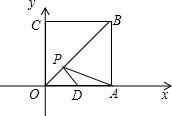 正方形OABC位于坐标系如图,边长为4,在OA上有一点坐标D(3,0)在对角线OB上有一动点P,使PA+PD最短,则最短距离为
正方形OABC位于坐标系如图,边长为4,在OA上有一点坐标D(3,0)在对角线OB上有一动点P,使PA+PD最短,则最短距离为 如图,南北向的公路上有一点A,东西向的公路上有一点B,若要在南北向的公路上确定点P,使得△PAB是等腰三角形,则这样的点P最多能确定 ( )个.
如图,南北向的公路上有一点A,东西向的公路上有一点B,若要在南北向的公路上确定点P,使得△PAB是等腰三角形,则这样的点P最多能确定 ( )个.