题目内容
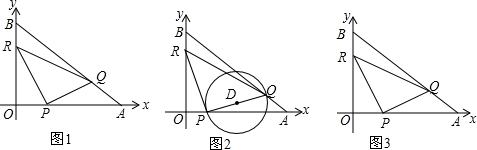
依据给定的条件，求一次函数的解析式．（1）已知一次函数的图象如图，求此一次函数的解析式，并判断点（6，5）是否在此函数图象上．
（2）已知一次函数y=2x+b的图象与y轴的交点到x轴的距离是4，求其函数解析式．
考点：待定系数法求一次函数解析式
专题：
分析：（1）根据图象知，该函数图象经过点（0，-8）、（4，0），所以把它们分别代入一次函数解析式y=kx+b（≠0），列出关于系数的方程组，通过解方程组可以求得该一次函数解析式，再进一步代入验证点（6，5）是否在此函数图象上；
（2）图象与y轴的交点到x轴的距离是4，说明图象经过点（0，4）或（0，-4），直接代入求得b的值，得出函数解析式即可．
（2）图象与y轴的交点到x轴的距离是4，说明图象经过点（0，4）或（0，-4），直接代入求得b的值，得出函数解析式即可．
解答：解：（1）设该直线解析式为y=kx+b（≠0）．
如图所示，该直线经过点（0，-8）、（4，0），则
，
解得
．
所以该直线方程为：y=2x-8．
把x=6代入y=2x-8=4，
所以点（6，5）不在此函数图象上．
（2）∵图象与y轴的交点到x轴的距离是4，
∴图象经过点（0，4）或（0，-4），
把（0，4）或（0，-4），分别代入y=2x+b，
解得b=-4或b=4
∴函数解析式为y=2x+4或y=2x-4．
如图所示，该直线经过点（0，-8）、（4，0），则
|
解得
|
所以该直线方程为：y=2x-8．
把x=6代入y=2x-8=4，
所以点（6，5）不在此函数图象上．
（2）∵图象与y轴的交点到x轴的距离是4，
∴图象经过点（0，4）或（0，-4），
把（0，4）或（0，-4），分别代入y=2x+b，
解得b=-4或b=4
∴函数解析式为y=2x+4或y=2x-4．
点评：本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；解方程或方程组，求出待定系数的值，进而写出函数解析式．
练习册系列答案
相关题目
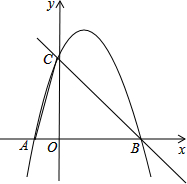如图，在平面直角坐标系中，点O为坐标原点，直线y=-x+n与x轴、y轴分别交于B、C两点，抛物线y=ax2+bx+3（a≠0）过C、B两点，交x轴于另一点A，连接AC，且tan∠CAO=3．点P是线段CB上一点（不和B、C重合），过点P作x轴的垂线，垂足为H，交抛物线于Q，
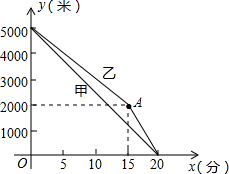甲、乙两名运动员进行长跑训练，两人距离终点的路程y（米）与跑步时间x（分）之间的关系如图所示，根据图象回答下列问题：
如图，如果“炮”所在的位置的坐标为（-3，1），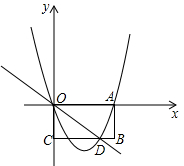
已知矩形OABC在平面直角坐标系中位置如图，点A的坐标为（6，0），点C的坐标为（0，-3），直线y=-