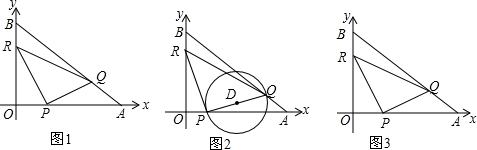
题目内容
 如图,四边形OABC为矩形,OA=4,OC=5,正比例函数y=2x的图象交AB于点D,连接DC,动点Q从D点出发沿DC向终点C运动,动点P从C点出发沿CO向终点O运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了ts.
如图,四边形OABC为矩形,OA=4,OC=5,正比例函数y=2x的图象交AB于点D,连接DC,动点Q从D点出发沿DC向终点C运动,动点P从C点出发沿CO向终点O运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了ts.(1)求△PCQ的面积S△PCQ=?(用t的代数式表示);
(2)问:是否存在时刻t使S△DOP=S△PCQ?为什么?
(3)当t为何值时,△DPQ是一个以DP为腰的等腰三角形?
考点:四边形综合题
专题:综合题
分析:(1)分别过点Q、D作QE⊥OC,DF⊥OC交OC与点E、F,对于直线y=2x,令y=4求出x的值,确定出D坐标,进而求出BD,BC的长,利用勾股定理求出CD的长,利用两对角相等的三角形相似得到三角形CQE与三角形CDF相似,由相似得比例表示出QE,由底PC,高QE表示出三角形PQC面积即可;
(2)不存在,理由为:表示出三角形ODP面积,令S△DOP=S△PCQ,求出t=5,此时Q与C重合,不能构成三角形;
(3)由三角形CQE与三角形CDF相似,利用相似得比例表示出CE,PE,进而利用勾股定理表示出PQ2,DP2,以及DQ,分两种情况考虑:①当DP=PQ;②当DP=DQ,求出t的值即可.
(2)不存在,理由为:表示出三角形ODP面积,令S△DOP=S△PCQ,求出t=5,此时Q与C重合,不能构成三角形;
(3)由三角形CQE与三角形CDF相似,利用相似得比例表示出CE,PE,进而利用勾股定理表示出PQ2,DP2,以及DQ,分两种情况考虑:①当DP=PQ;②当DP=DQ,求出t的值即可.
解答: 解:(1)分别过点Q、D作QE⊥OC,DF⊥OC交OC与点E、F,
解:(1)分别过点Q、D作QE⊥OC,DF⊥OC交OC与点E、F,
对于直线y=2x,令y=4,得到x=2,即D(2,4),
∴BD=OC-AD=5-2=3,
∵BC=OA=4,
∴在Rt△BCD中,根据勾股定理得:CD=
=5,
∵∠DCF=∠QCE,∠DFC=∠QEC=90°,
∴△CQE∽△CDF,
∴
=
,即
=
,
∴QE=
,
则S△CPQ=
×t×
(5-t)=
t(5-t)=-
t2+2t;
(2)不存在,理由为:
根据题意得:S△ODP=
×4×(5-t)=2(5-t),
令2(5-t)=-
t2+2t,
解得:t1=t2=5,
则此时Q与C重合,不能构成三角形;
(3)∵△CQE∽△CDF,
∴CE=
(5-t),PE=t-
(5-t)=
t-3,
∴根据勾股定理得:PQ2=
+(
t-3)2=
t2-16t+25,DP2=42+(3-t)2,DQ=t,
分两种情况考虑:
①当DP=PQ时,42+(3-t)2=
t2-16t+25,
解得:t1=0(舍去),t2=
;
②当DP=DQ时,42+(3-t)2=t2,
解得:t=
,
答:当t=
或t=
时,△DPQ是一个以DP为腰的等腰三角形.
 解:(1)分别过点Q、D作QE⊥OC,DF⊥OC交OC与点E、F,
解:(1)分别过点Q、D作QE⊥OC,DF⊥OC交OC与点E、F,对于直线y=2x,令y=4,得到x=2,即D(2,4),
∴BD=OC-AD=5-2=3,
∵BC=OA=4,
∴在Rt△BCD中,根据勾股定理得:CD=
| BD2+BC2 |
∵∠DCF=∠QCE,∠DFC=∠QEC=90°,
∴△CQE∽△CDF,
∴
| CQ |
| CD |
| QE |
| DF |
| 5-t |
| 5 |
| QE |
| 4 |
∴QE=
| 4(5-t) |
| 5 |
则S△CPQ=
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
(2)不存在,理由为:
根据题意得:S△ODP=
| 1 |
| 2 |
令2(5-t)=-
| 2 |
| 5 |
解得:t1=t2=5,
则此时Q与C重合,不能构成三角形;
(3)∵△CQE∽△CDF,
∴CE=
| 3 |
| 5 |
| 3 |
| 5 |
| 8 |
| 5 |
∴根据勾股定理得:PQ2=
| 16(5-t)2 |
| 25 |
| 8 |
| 5 |
| 16 |
| 5 |
分两种情况考虑:
①当DP=PQ时,42+(3-t)2=
| 16 |
| 5 |
解得:t1=0(舍去),t2=
| 50 |
| 11 |
②当DP=DQ时,42+(3-t)2=t2,
解得:t=
| 25 |
| 6 |
答:当t=
| 25 |
| 6 |
| 50 |
| 11 |
点评:此题属于四边形综合题,涉及的知识有:坐标与图形性质,相似三角形的判定与性质,勾股定理,以及等腰三角形的性质,熟练掌握相似三角形的判定与性质以及勾股定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知⊙O的直径AB垂直于弦CD于E,连结AD,BD,OC,OD,且OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连结AD,BD,OC,OD,且OD=5. 如图,在折成ABCDEF中,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M,试探索∠M与∠3的关系,说明理由.
如图,在折成ABCDEF中,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M,试探索∠M与∠3的关系,说明理由.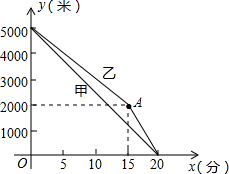 甲、乙两名运动员进行长跑训练,两人距离终点的路程y(米)与跑步时间x(分)之间的关系如图所示,根据图象回答下列问题:
甲、乙两名运动员进行长跑训练,两人距离终点的路程y(米)与跑步时间x(分)之间的关系如图所示,根据图象回答下列问题: 如图,如果“炮”所在的位置的坐标为(-3,1),
如图,如果“炮”所在的位置的坐标为(-3,1), 已知矩形OABC在平面直角坐标系中位置如图,点A的坐标为(6,0),点C的坐标为(0,-3),直线y=-
已知矩形OABC在平面直角坐标系中位置如图,点A的坐标为(6,0),点C的坐标为(0,-3),直线y=-