题目内容
5. 如图,在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=BF,连接AE,EF和CF.求证:
如图,在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,BE=BF,连接AE,EF和CF.求证:(1)AE=CF.
(2)AE⊥CF.
分析 (1)根据SAS证明△ABE≌△CBF即可得出AE=CF;
(2)先延长AE交CF于D,根据三角形的内角和得:∠CDE=∠ABC=90°,则AE⊥CF.
解答 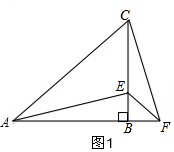 证明:(1)如图1,∵∠ABC=90°,
证明:(1)如图1,∵∠ABC=90°,
∴∠ABC=∠EBF=90°,
在△ABE和△CBF中,
∵$\left\{\begin{array}{l}{AB=BC}\\{∠ABC=∠EBF}\\{BE=BF}\end{array}\right.$,
∴△ABE≌△CBF(SAS),
∴AE=CF;
(2)如图2,延长AE交CF于D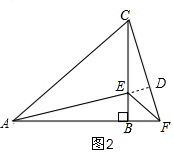 ,
,
∵△ABE≌△CBF,
∴∠BAE=∠BCF,
∵∠AEB=∠CED,
∴∠CDE=∠ABC=90°,
∴AD⊥CF,
即AE⊥CF.
点评 本题考查了全等三角形的判定和性质和等腰直角三角形的性质,做好本题要熟练掌握全等的判定方法:SSS、ASA、AAS、SAS;在几何证明中,常利用两个三角形中有两个角对应相等,根据三角形的内角和定理,得第三个角对应相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目