Question

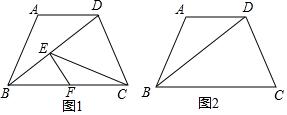
2．在△ABC中，∠C＞∠B．
（1）如图①，AD⊥BC于点D，AE平分∠BAC，证明：∠EAD=$\frac{1}{2}$（∠C-∠B）．
（2）如图②，AE平分∠BAC，F为AE上的一点，且FD⊥BC于点D，这时∠EFD与∠B、∠C有何数量关系？请说明理由；
（3）如图③，AE平分∠BAC，F为AE延长线上的一点，FD⊥BC于点D，请你写出这时∠AFD与∠B、∠C之间的数量关系（只写结论，不必说明理由）．

Answer 1

分析 （1）由图不难发现∠EAD=∠EAC-∠DAC，再根据三角形的内角和定理及其推论结合角平分线的定义分别用结论中出现的角替换∠EAC和∠DAC．
（2）（2）由角平分线的性质和三角形的内角和得出∠BAE=90°-$\frac{1}{2}$（∠C+∠B），外角的性质得出∠AEC=90°+$\frac{1}{2}$（∠B-∠C），在△EFD中，由三角形内角和定理可得∠EFD；
（3）与（2）的方法相同．

解答 证明：（1）∵AE平分∠BAC，
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC
∵∠BAC=180°-（∠B+∠C）
∴∠EAC=$\frac{1}{2}$[180°-（∠B+∠C）]
∵AD⊥BC，
∴∠ADC=90°，
∴∠DAC=180°-∠ADC-∠C=90°-∠C，
∵∠EAD=∠EAC-∠DAC
∴∠EAD=$\frac{1}{2}$[180°-（∠B+∠C）]-（90°-∠C）=$\frac{1}{2}$（∠C-∠B）．

（2）∠EFD=$\frac{1}{2}$（∠C-∠B）
∵AE平分∠BAC，
∴∠BAE=$\frac{180°-∠B-∠C}{2}$=90°-$\frac{1}{2}$（∠C+∠B），
∵∠AEC为△ABE的外角，
∴∠AEC=∠B+90°-$\frac{1}{2}$（∠C+∠B）=90°+$\frac{1}{2}$（∠B-∠C），
∵FD⊥BC，
∴∠FDE=90°．
∴∠EFD=90°-90°-$\frac{1}{2}$（∠B-∠C）
∴∠EFD=$\frac{1}{2}$（∠C-∠B）

（3）∠EFD=$\frac{1}{2}$（∠C-∠B）．
∵AE平分∠BAC，
∴∠BAE=$\frac{180°-∠B+∠C}{2}$．
∵∠DEF为△ABE的外角，
∴∠DEF=∠B+$\frac{180°-∠B+∠C}{2}$=90°+$\frac{1}{2}$（∠B-∠C），
∵FD⊥BC，
∴∠FDE=90°．
∴∠EFD=90°-90°-$\frac{1}{2}$（∠B-∠C），
∴∠EFD=$\frac{1}{2}$（∠C-∠B）．

点评 本题主要考查了三角形的内角和定理，综合利用角平分线的性质和三角形内角和定理是解答此题的关键．