题目内容
9.直角三角形的两条直角边分别是3$\sqrt{6}$,3$\sqrt{3}$,则斜边上的高为3$\sqrt{2}$.分析 根据勾股定理可以求得斜边的长,然后根据等积法可以求得斜边上的高.
解答 解:∵直角三角形的两条直角边分别是3$\sqrt{6}$,3$\sqrt{3}$,
∴斜边长为:$\sqrt{(3\sqrt{6})^{2}+(3\sqrt{3})^{2}}=9$,
∴斜边上的高为:$\frac{3\sqrt{6}×3\sqrt{3}}{9}=3\sqrt{2}$,
故答案为:3$\sqrt{2}$.
点评 本题考查二次根式的应用,解答本题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
4.一个寻宝游戏的通道平面图如图1所示(正方形ABCD是⊙O的内接四边形),图中的所有线段和弧线都是通道.为了记录寻宝者的行进路线,相关人员在点O处放置了一台定位仪器.设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x之间的函数关系的图象如图2所示,则寻宝者的行进路线可能为…( )
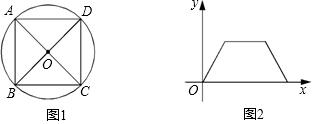

| A. | 线段OA→劣弧AD→线段DO | B. | 劣弧AD→线段DO→线段OC | ||
| C. | 劣弧AD→劣弧DC→线段CO | D. | 线段OB→劣弧BC→劣弧CD |
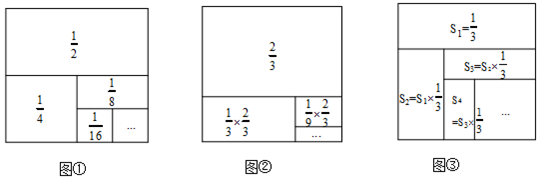
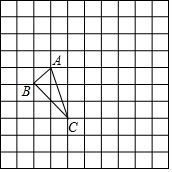 如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.
如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.