题目内容
1．
如图，圆弧形桥拱的跨度AB=16米，拱高CD=4米，那么圆弧形桥拱所在圆的半径是10米．
分析 根据题意构造直角三角形，进而利用勾股定理求出答案．
解答 
解：设圆弧形桥拱所在圆心为O，连接BO，DO，
可得：AD=BD，OD⊥AB，
∵AB=16米，拱高CD=4米，
∴BD=AD=8m，
设BO=xm，则DO=（x-4）m，
根据题意可得：BD2+DO2=BO2，
即82+（x-4）2=x2，
解得：x=10，
即圆弧形桥拱所在圆的半径是10m．
故答案为：10．
点评 此题主要考查了垂径定理的应用以及勾股定理，正确应用垂径定理是解题关键．
练习册系列答案
相关题目
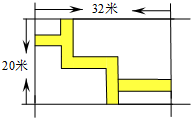如图，某居民小区有一长方形地，居民想在长方形地内修筑同样宽的小路，小路的宽为2米，余下部分绿化，为了使草坪更美观，有人建议把道路进行如图所示的修筑方案，求绿化的面积为多少平方米？
12．在海上，一座灯塔位于一艘船的北偏东40°方向，那么这艘船位于灯塔（ ）
| A． | 南偏西50°方向 | B． | 南偏西40°方向 | C． | 北偏东50°方向 | D． | 北偏东40°方向 |
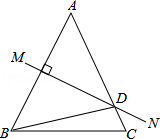如图，等腰△ABC中，AB=AC，∠BAC=50°，AB的垂直平分线MN交AC于点D，则∠DBC的度数是15°．
如图，已知⊙O的半径为30mm，若AB=36mm，则点O到AB的距离为24mm．
如图，点D、E分别是△ABC的边AC、BC上的点，AD=DE，AB=BE，∠A=80°，则∠BED=80°．
如图，在五边形ABCDE中，若∠1+∠2+∠3+∠4=280°，则∠D=100°．