题目内容
2.分解因式:(1)x4-y4
(2)a3b-ab
(3)a3-a
(4)-(1+xy)2+(1-xy)2
(5)(x+p)2-(x+q)2.
分析 (1)利用平方差公式因式分解;
(2)(3)先提取公因式,再进一步利用平方差公式因式分解;
(4)(5)利用平方差公式分解因式.
解答 解:(1)原式=(x2-y2)(x2+y2)
=(x+y)(x-y)(x2+y2);
(2)原式=ab(a2-1)
=ab(a+1)(a-1);
(3)原式=a(a2-1)
=a(a+1)(a-1);
(4)原式=[-(1+xy)+(1-xy)][(1+xy)+(1-xy)]
=-2xy×2
=-4xy;
(5)原式=(x+p+x+q)(x+p-x-q)
=(2x+p+q)(p-q).
点评 本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
12.已知两相似三角形的面积比是4:25,则它们的周长的比为( )
| A. | 4:25 | B. | 2:5 | C. | 1:5 | D. | 以上都不对 |
13.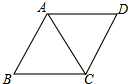 如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
 如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
10.下列实数中属于无理数的是( )
| A. | $\frac{3}{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{9}$ | D. | $\root{3}{-\frac{1}{27}}$ |