题目内容
11. 四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AC=BD.试添加一个条件AB∥CD(答案不唯一),使四边形ABCD为矩形.
四边形ABCD的对角线AC、BD相交于点O,AD∥BC,AC=BD.试添加一个条件AB∥CD(答案不唯一),使四边形ABCD为矩形.
分析 先证明四边形ABCD是平行四边形,再由对角线相等,即可得出结论.
解答 解:添加条件AB∥CD,使四边形ABCD为矩形;理由如下:
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD为矩形;
故答案为:AB∥CD(答案不唯一).
点评 本题考查了矩形的判定、平行四边形的判定;熟练掌握矩形的判定方法,证明四边形是平行四边形是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
2.若x1、x2是方程x2-2x-1=0的两个根,则x1+x1x2+x2的值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
19.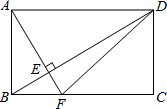 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
 如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )
如图,在矩形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,则图中面积相等但不全等的三角形共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
6.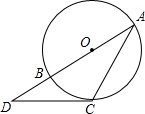 如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
 如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )
如图,⊙O的直径AB=2,点D在AB的延长线上,DC与⊙O相切于点C,连接AC.若∠A=30°,则CD长为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
3.在Rt△ABC中,∠C=90°,sinA=$\frac{3}{5}$,b=4,则tanB=( )
| A. | $\frac{4}{5}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
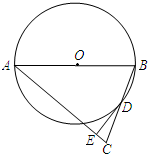 如图,已知△ABC中,AB=AC,以AB为直径的⊙O与BC边相交于点D,⊙O的切线DE交AC于点E.
如图,已知△ABC中,AB=AC,以AB为直径的⊙O与BC边相交于点D,⊙O的切线DE交AC于点E. 如图,已知平面直角坐标系中存在点M(2,0),点A(a,0).在x轴负半轴上有点C,且满足AM=OC,现以AC为对角线作正方形ABCD,设AM的中点为P,当以点O为圆心,OP为半径的圆与正方形ABCD的边相切时,a的值是2$\sqrt{2}$+2或6+4$\sqrt{2}$或6-4$\sqrt{2}$.
如图,已知平面直角坐标系中存在点M(2,0),点A(a,0).在x轴负半轴上有点C,且满足AM=OC,现以AC为对角线作正方形ABCD,设AM的中点为P,当以点O为圆心,OP为半径的圆与正方形ABCD的边相切时,a的值是2$\sqrt{2}$+2或6+4$\sqrt{2}$或6-4$\sqrt{2}$. 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线的y=$\frac{k}{x}$(k>0)图象经过点A,若△BEC的面积为4,则k=8.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线的y=$\frac{k}{x}$(k>0)图象经过点A,若△BEC的面积为4,则k=8.