题目内容
6．
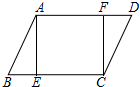在?ABCD中，AB=5，BC=7，E，F分别为边BC，AD上的点，若四边形AECF为正方形，则AE的长为（ ）| A． | 5 | B． | 4或5 | C． | 3或4 | D． | 5或7 |
分析 首先设AE=x，由四边形AECF为正方形，可得CE=AE=x，∠AEB=90°，然后由勾股定理得方程：52=x2+（7-x）2，继而求得答案．
解答 解：设AE=x，
∵四边形AECF为正方形，
∴CE=AE=x，∠AEB=90°，
∴BE=BC-CE=7-x，
在Rt△ABE中，BE2+AE2=AB2，
∴52=x2+（7-x）2，
解得：x=3或4，
∴AE=3或4．
故选C．
点评 此题考查了正方形的性质、勾股定理以及平行四边形的性质．注意利用方程思想求解是解此题的关键．
练习册系列答案
相关题目
如图，已知平面直角坐标系中存在点M（2，0），点A（a，0）．在x轴负半轴上有点C，且满足AM=OC，现以AC为对角线作正方形ABCD，设AM的中点为P，当以点O为圆心，OP为半径的圆与正方形ABCD的边相切时，a的值是2$\sqrt{2}$+2或6+4$\sqrt{2}$或6-4$\sqrt{2}$．
14．
一个简单空间几何体的三视图如图所示，则这个几何体是（ ）
一个简单空间几何体的三视图如图所示，则这个几何体是（ ）| A． | 三棱锥 | B． | 四棱锥 | C． | 三棱柱 | D． | 四棱柱 |
如图，Rt△ABC的直角边BC在x轴上，斜边AC上的中线BD交y轴于点E，双曲线的y=$\frac{k}{x}$（k＞0）图象经过点A，若△BEC的面积为4，则k=8．
11．-$\frac{3}{4}$的倒数是（ ）
| A． | -$\frac{4}{3}$ | B． | $\frac{4}{3}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |
15．下列各数中，无理数的是（ ）
| A． | $\frac{22}{7}$ | B． | ${（{\sqrt{5}}）^0}$ | C． | π | D． | $\sqrt{4}$ |
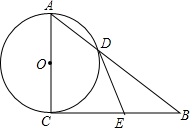如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，点E是BC的中点，连结DE．