题目内容
6.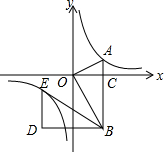 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.
分析 (1)将点A($\sqrt{3}$,1)代入y=$\frac{k}{x}$,利用待定系数法即可求出反比例函数的表达式;
(2)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(-$\sqrt{3}$,-1),即可求解.
解答 解:(1)∵点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=$\sqrt{3}$×1=$\sqrt{3}$.
(2)点E在该反比例函数的图象上,理由如下:
∵A($\sqrt{3}$,1),
∴OA=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2,
由OA⊥OB,AB⊥x轴,易证△AOC∽△ABO,
∴$\frac{AO}{AB}$=$\frac{AC}{AO}$,即$\frac{2}{AB}$=$\frac{1}{2}$,
∴AB=4,
∴OB=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴sin∠ABO=$\frac{OA}{AB}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠ABO=30°.
∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,
∴△BOA≌△BDE,∠OBD=60°,
∴BO=BD=2$\sqrt{3}$,OA=DE=2,∠BOA=∠BDE=90°,
∠ABD=30°+60°=90°.
又BD-OC=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$,BC-DE=4-1-2=1,
∴E(-$\sqrt{3}$,-1),
∵-$\sqrt{3}$×$(-1)=\sqrt{3}$,
∴点E在该反比例函数的图象上.
点评 本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,旋转的性质,正确求出解析式是解题的关键.

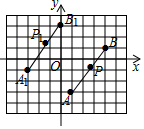 如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
如图,线段AB经过平移得到线段A1B1,其中A、B的对应点分别为A1、B1,这四个点都在格点上,若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )| A. | (a-4,b+2) | B. | (a-4,b-2) | C. | (a+4,b+2) | D. | (a+4,b-2) |
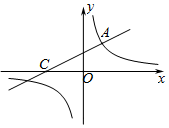 如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.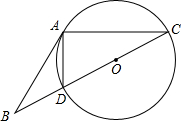 如图,△ABC中,O为BC上一点,⊙O过A,C两点交BC于D,BA为⊙O的切线,若sin∠B=$\frac{3}{5}$,求tan∠BAD的值.
如图,△ABC中,O为BC上一点,⊙O过A,C两点交BC于D,BA为⊙O的切线,若sin∠B=$\frac{3}{5}$,求tan∠BAD的值.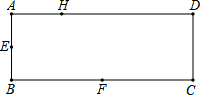 如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( )
如图,矩形ABCD的长和宽分别为3和1,点E、F分别是AB、BC边的中点,点H在矩形ABCD边上,则使△EFH为直角三角形的点H的个数为( )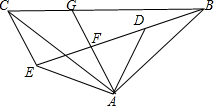 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( )
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,所给结论:①∠BAD=∠CAE;②tan∠ABE=$\frac{\sqrt{3}}{3}$;③AG∥CE;④2AF+CE=BE;⑤AD=CG中,正确的有( ) 如图,在△ABC中,AB=AC,∠A=36°,线段AB的垂直平分线MN分别交AB、AC于N、M.
如图,在△ABC中,AB=AC,∠A=36°,线段AB的垂直平分线MN分别交AB、AC于N、M.