题目内容
14.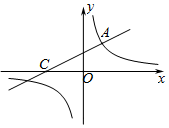 如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.
如图,直线y=$\frac{1}{2}$x+2与双曲线相交于点A(m,3),与x轴交于点C.(1)求双曲线解析式;
(2)根据图象直接写出,在什么范围时,一次函数的值小于反比例函数的值;
(3)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
分析 (1)把A坐标代入直线解析式求出m的值,确定出A坐标,即可确定出双曲线解析式;
(2)联立一次函数与反比例函数解析式求出交点坐标,利用图象确定出一次函数值小于反比例函数值时x的范围即可.
(3)设P(x,0),表示出PC的长,高为A纵坐标,根据三角形ACP面积求出x的值,确定出P坐标即可.
解答 解:(1)把A(m,3)代入直线解析式得:3=$\frac{1}{2}$m+2,即m=2,
∴A(2,3),
把A坐标代入y=$\frac{k}{x}$,得k=6,
则双曲线解析式为y=$\frac{6}{x}$;
(2)联立一次函数与反比例函数解析式得,
$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{\;}\\{y=\frac{1}{2}x+2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{\;}\\{y=3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-6}\\{\;}\\{y=-1}\end{array}\right.$,
∴一次函数的值小于反比例函数的值时x的范围是:x<-6或x>2;
(3)对于直线y=$\frac{1}{2}$x+2,令y=0,得到x=-4,即C(-4,0),
设P(x,0),可得PC=|x+4|,
∵△ACP面积为3,
∴$\frac{1}{2}$|x+4|•3=3,即|x+4|=2,
解得:x=-2或x=-6,
则P坐标为(-2,0)或(-6,0).
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:待定系数法确定函数解析式,坐标与图形性质,以及三角形面积求法,熟练掌握待定系数法是解本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 平分弦的直径垂直弦 | |
| C. | 有两边及一角对应相等的两个三角形全等 | |
| D. | 八边形的内角和是外角和的3倍 |
| A. | x>5 | B. | x≥5 | C. | x≠5 | D. | 全体实数 |
| A. | tan x | B. | sin x | C. | cosx | D. | cotx |
 如图,AB是圆O的直径,DB,DC分别切圆O于点B,C,若∠ACE=25°,则∠D的度数是( )
如图,AB是圆O的直径,DB,DC分别切圆O于点B,C,若∠ACE=25°,则∠D的度数是( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |

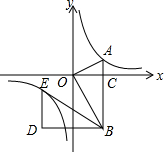 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.