题目内容
16．在平面直角坐标系中，点A（2，0），B（0，-3），若$\overrightarrow{OA}$$+\overrightarrow{OB}$=$\overrightarrow{OC}$，则点C的坐标为（2，-3）．分析 根据平面向量的平行四边形的法则解答即可得．
解答 解：如图，
∵$\overrightarrow{OA}$$+\overrightarrow{OB}$=$\overrightarrow{OC}$，
∴过点A作y轴的平行线，过点B作x中的平行线，交于点C，则点C（2，-3），
故答案为：（2，-3）．
点评 本题主要考查平面向量，熟练掌握平面向量的平行四边形法则是解题的关键．
练习册系列答案
相关题目
7．
如图，D是等边△ABC外接圆上的点，且∠DAC=20°，则∠ACD的度数为（ ）
如图，D是等边△ABC外接圆上的点，且∠DAC=20°，则∠ACD的度数为（ ）| A． | 20° | B． | 30° | C． | 40° | D． | 45° |
4．下列命题中，真命题是（ ）
| A． | 垂直于同一条直线的两条直线互相平行 | |
| B． | 平分弦的直径垂直弦 | |
| C． | 有两边及一角对应相等的两个三角形全等 | |
| D． | 八边形的内角和是外角和的3倍 |
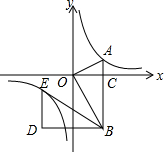如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（$\sqrt{3}$，1）在反比例函数y=$\frac{k}{x}$的图象上．