题目内容
5.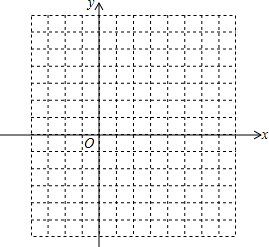 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
分析 (1)利用配方法将一次项和二次项组合,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
(2)将已知方程转化为两点式方程即可得到该抛物线与x轴的交点坐标;令x=0即可得到该抛物线与y轴交点的纵坐标;
(3)将抛物线y=x2-2x-3上的点的坐标列出,然后在平面直角坐标系中找出这些点,连接起来即可;
(4)结合图象可以直接得到答案.
解答 解:(1)y=x2-2x-3=x2-2x+1-3-1=(x-1)2-4,即y=(x-1)2-4;
(2)令x=0,则y=-3,即该抛物线与y轴的交点坐标是 (0,-3),
又y=x2-2x-3=(x-3)(x+1),
所以该抛物线与x轴的交点坐标是(3,0)(-1,0).
故答案是:(0,-3);(3,0)(-1,0);
(3)列表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | 0 | … |
 ;
;(4)如图所示,不等式x2-2x-3>0的解集是x<-1或x>3.
故答案是:x<-1或x>3.
点评 本题考查了二次函数的三种形式、二次函数的对称性和由函数图象确定坐标、直线与图象的交点问题,综合体现了数形结合的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
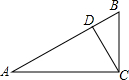 如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长.
如图,△ABC中,∠ACB=90°,BC=8,AC=12,∠BCD=30°,求线段CD长. 某水渠的横截面呈抛物线形,水面的宽为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.设坐标原点为O,已知水面的宽AB=8米,设抛物线解析式为y=ax2-4.
某水渠的横截面呈抛物线形,水面的宽为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.设坐标原点为O,已知水面的宽AB=8米,设抛物线解析式为y=ax2-4.