题目内容
20.计算:(1)($\sqrt{3}$-1)0-2cos30°-($\frac{1}{8}$)-1+$\sqrt{12}$;
(2)sin215°+cos215°-cos60°tan60°+$\frac{1}{sin60°-1}$.
分析 (1)根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式=1-2×$\frac{\sqrt{3}}{2}$-8+2$\sqrt{3}$,然后合并即可;
(2)利用三角函数公式和特殊角的三角函数值得到原式=1-$\frac{1}{2}$×$\sqrt{3}$+$\frac{1}{\frac{\sqrt{3}}{2}-1}$,然后分母有理化后合并即可.
解答 解:(1)原式=1-2×$\frac{\sqrt{3}}{2}$-8+2$\sqrt{3}$
=$\sqrt{3}$-7;
(2)原式=1-$\frac{1}{2}$×$\sqrt{3}$+$\frac{1}{\frac{\sqrt{3}}{2}-1}$
=1-$\frac{\sqrt{3}}{2}$-2(2+$\sqrt{3}$)
=1-$\frac{\sqrt{3}}{2}$-4-2$\sqrt{3}$
=-3-$\frac{7\sqrt{3}}{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
 a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )| A. | 2a-b | B. | b | C. | -b | D. | -2a+b |
5.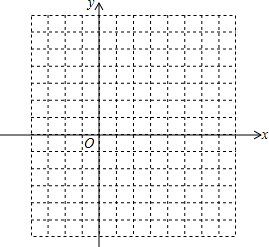 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.
(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
(4)不等式x2-2x-3>0的解集是x<-1或x>3.
 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
9. 如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )
如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )
 如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )
如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )| A. | m+n>0 | B. | m+n<0 | C. | m-n>0 | D. | m-n=0 |
 如图,△ABC中,∠ACB=90°,AC=BC,AD⊥CD于D,BE⊥CD于E,BE=2.5cm,DE=1.7cm,求AD的长.
如图,△ABC中,∠ACB=90°,AC=BC,AD⊥CD于D,BE⊥CD于E,BE=2.5cm,DE=1.7cm,求AD的长.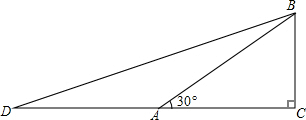 若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?
若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?