题目内容
16.解方程(1)x2-2x-1=0
(2)(x-3)2-2x(3-x)=0.
分析 (1)利用配方法求得方程的解即可;
(2)利用因式分解法解方程即可.
解答 解:(1)x2-2x-1=0
x2-2x=1
x2-2x+1=2
(x-1)2=2
x-1=±$\sqrt{2}$
解得:x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$;
(2)(x-3)2-2x(3-x)=0
(x-3)(x-3+2x)=0
x-3=0,3x-3=0,
解得:x1=3,x2=1.
点评 本题考查了利用配方法和因式分解法解一元二次方程,解此题的关键是能根据方程的特点选择适当的方法解一元二次方程.

练习册系列答案
相关题目
5.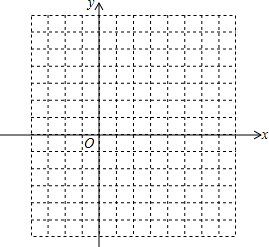 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.
(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
(4)不等式x2-2x-3>0的解集是x<-1或x>3.
 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
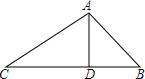 先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.
先阅读材料.再解答下面的问题:问题:在△ABC中,AD是边BC上的高,AD=2,DB=2,CD=2$\sqrt{3}$,求∠BAC的度数.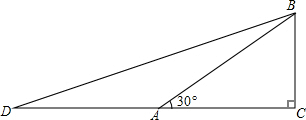 若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?
若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?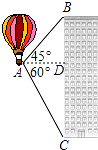 如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).
如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).