题目内容
13.已知抛物线y=x2+bx+c的对称轴为y轴,且过点C(0,-4).(1)求此抛物线的解析式;
(2)若点(-2,y1)与(3,y2)都在此抛物线上,则y1<y2.(填“>”、“=”或“<”)
分析 (1)利用对称轴方程可得b=0,利用抛物线与y轴的交点可得到c的值,于是可确定抛物线解析式;
(2)把点(-2,y1)与(3,y2)都代入(1)中的解析式计算出y1和y2的值,然后比较大小.
解答 解:(1)∵抛物线的对称轴为y轴,
∴b=0.
又∵抛物线过点(0,-4),
∴c=3.
∴抛物线的解析式为y=x2-4;
(2)当x=-2时,y1=x2-4=0,
当x=3时,y2=x2-4=5,
∴y1<y2.
故答案为<.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
3.某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午13:00~17:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品的件数与所用时间之间的关系如下表:
信息三:按件计酬,每生产一件甲产品可得1.5元,每生产一件乙产品可得2.80元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟?
(2)若小王每月生产甲产品a件,乙产品b件,当a、b分别是多少时,小王收入最多?
信息一:工作时间:每天上午8:00~12:00,下午13:00~17:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品的件数与所用时间之间的关系如下表:
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(min) |
| 10 | 10 | 350 |
| 30 | 20 | 850 |
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分钟?
(2)若小王每月生产甲产品a件,乙产品b件,当a、b分别是多少时,小王收入最多?
5.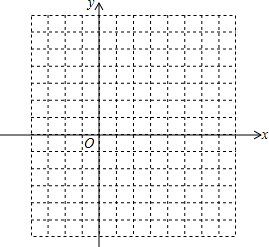 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.
(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
(4)不等式x2-2x-3>0的解集是x<-1或x>3.
 已知二次函数y=x2-2x-3.
已知二次函数y=x2-2x-3.(1)将y=x2-2x-3化成y=a(x-h)2+k的形式;
(2)与y轴的交点坐标是(0,-3),与x轴的交点坐标是(3,0)(-1,0);
(3)在坐标系中利用描点法画出此抛物线.
| x | … | … | |||||
| y | … | … |
2.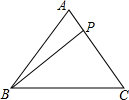 如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
 如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )
如图,在△ABC中,有一点P在直线AC上移动,若AB=AC=5,BC=6,则BP的最小值为( )| A. | 4.8 | B. | 5 | C. | 4 | D. | $\sqrt{24}$ |
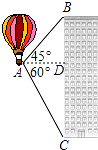 如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).
如图,热气球的探测器在点A,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为30米,求这栋楼的高度($\sqrt{3}$取1.73,结果精确到0.1米).