题目内容
9.如果一组数据a1,a2,…,an的方差是2,那么一组新数据2a1+1,2a2+1,…,2an+1的方差是( )| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
分析 设已知数据的平均数为$\overline{a}$,根据数据的方差列出关系式,进而求出新数据的平均数,得出方差即可.
解答 解:∵一组数据a1,a2,…,an的方差是2,平均数为$\overline{a}$,
∴S2=$\frac{1}{n}$[(a1-$\overline{a}$)2+(a2-$\overline{a}$)2+…+(an-$\overline{a}$)2]=2,
∵2a1+1,2a2+1,…,2an+1的平均数为2$\overline{a}$+1,
∴S′2=$\frac{1}{n}$[(2a1+1-2$\overline{a}$-1)2+(2a2+1-2$\overline{a}$-1)2+…+(2an+1-2$\overline{a}$-1)2]=2×22=8,
故选:D
点评 此题考查了方差,以及平均数,熟练掌握各自的算法是解本题的关键.

练习册系列答案
相关题目
16.若代数式$\frac{\sqrt{2-x}}{1+x}$有意义,则x的取值范围是( )
| A. | x≥-2且x≠-1 | B. | x>-2且x≠-1 | C. | x≤2且x≠-1 | D. | x<2且x≠-1 |
17.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
17.某技工培训中心有钳工20名、车工30名.现将这50名技工中的15人派往A地工作,35人派往B地工作,两地技工的工资情况如下表:
设派往A地x名钳工时,这50名技工的月工资总额为y元.
(1)派往B地20-x名钳工,派往B地15+x名车工;
(2)求y关于x的函数关系式;
(3)若A地钳工的月工资总额不小于B地钳工的月工资总额,派往A地多少名钳工,可使这50名技工的月工资总额最高?
| 工种 属地 | 钳工 | 车工 |
| A地 | 1800(元/月) | 1600(元/月) |
| B地 | 1600(元/月) | 1200(元/月) |
(1)派往B地20-x名钳工,派往B地15+x名车工;
(2)求y关于x的函数关系式;
(3)若A地钳工的月工资总额不小于B地钳工的月工资总额,派往A地多少名钳工,可使这50名技工的月工资总额最高?
14.二次函数y=x2+px+q中,由于二次项系数为1>0,所以在对称轴左侧,y随x增大而减小,从而得到y越大则x越小,在对称轴右侧,y随x增大而减大,从而得到y越大则x也越大,请根据你对这句话的理解,解决下面问题:若关于x的方程x2+px+q+1=0的两个实数根是m、n(m<n),关于x的方程x2+px+q-5=0的两个实数根是d、e(d<e),则m、n、d、e的大小关系是( )
| A. | m<d<e<n | B. | d<m<n<e | C. | d<m<e<n | D. | m<d<n<e |
19.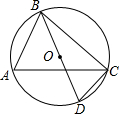 如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
 如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
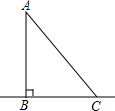 某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.
某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.