题目内容
19.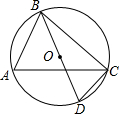 如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=4,∠A=60°,则BC的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 根据圆周角定理得∠BCD=90°,∠D=∠A=60°,然后利用∠D的正弦计算BC的长.
解答 解:∵BD为直径,
∴∠BCD=90°,
∵∠D=∠A=60°,
∴sinD=sin60°=$\frac{BC}{4}$,
∴BC=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
故选C.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
相关题目
10.已知x=-1是关于x的方程x2-x+m=0的一个根,则m的值为( )
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
7.若x1,x2是方程x2=4的两根,则x1+x2的值是( )
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
14.某人沿坡度i=1:$\sqrt{3}$的坡面向上走50米,则此人离地面的高度为( )
| A. | 25米 | B. | 50米 | C. | 25$\sqrt{3}$米 | D. | 50$\sqrt{3}$米 |
4.正多边形的中心角是36°,那么这个正多边形的边数为( )
| A. | 10 | B. | 8 | C. | 6 | D. | 5 |
11.下列结论不正确的是( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | B. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | ||
| C. | 如果$\overrightarrow{AB}$=$\overrightarrow{CD}$,那么|$\overrightarrow{AB}$|=|$\overrightarrow{CD}$| | D. | 如果非零向量$\overrightarrow{a}$=k$\overrightarrow{b}$(k≠0),那么$\overrightarrow{a}$∥$\overrightarrow{b}$ |
9.为了解峨边今年参加中考的1000名学生的体重情况,抽查了其中200名学生的体重进行统计分析,下列叙述正确的是( )
| A. | 200名学生是总体 | |
| B. | 200名学生的体重是总体的一个样本 | |
| C. | 每名学生是总体的一个个体 | |
| D. | 以上调查是普查 |