题目内容
18．
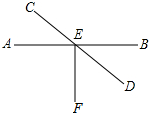如图，AB、CD相交于点E，EF平分∠AEB，若∠BED：∠DEF=2：3，则∠BEC的度数为（ ）| A． | 144° | B． | 126° | C． | 150° | D． | 72° |
分析 根据角平分线的定义求出∠BEF=90°，根据题意求出∠BED的度数，根据邻补角的概念计算即可．
解答 解：∵EF平分∠AEB，
∴∠BEF=90°，
∵∠BED：∠DEF=2：3，
∴∠BED=36°，
∴∠BEC=180°-∠BED=144°．
故选：A．
点评 本题考查的是对顶角、邻补角的概念和性质以及角平分线的定义，掌握邻补角之和等于180°是解题的关键．
练习册系列答案
相关题目
如图，为了测量某建筑物AB的高度，在地面上的C处测得建筑物顶端A的仰角为30°，沿CB方向前进30m到达D处，在D处测得建筑物顶端A的仰角为45°，则建筑物AB的高度等于15（$\sqrt{3}+1$）m．
6．下列根式是最简二次根式的是（ ）
| A． | $\sqrt{24}$ | B． | $\sqrt{{x}^{2}-1}$ | C． | $\sqrt{\frac{1}{2}}$ | D． | $\sqrt{{a}^{3}b}$ |
13．
如图，已知AD=AB，那么添加下列一个条件后，则无法判定△AED≌△ACB的是（ ）
如图，已知AD=AB，那么添加下列一个条件后，则无法判定△AED≌△ACB的是（ ）| A． | AE=AC | B． | DE=BC | C． | ∠E=∠C | D． | ∠ABC=∠ADE |
3．
有理数a，b，c在数轴上的位置如图所示，则|a+c|-|c-b|-|a+b|=（ ）
有理数a，b，c在数轴上的位置如图所示，则|a+c|-|c-b|-|a+b|=（ ）| A． | 0 | B． | 2a+2b | C． | -2a-2c | D． | 2b-2c |
一次函数y=kx+4的图象经过点（-3，-2）．
如图，△ABE为等腰直角三角形，∠ABE=90°，BC=BD，∠FAD=30°．