题目内容
2. (1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;
(1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;(2)写出点A1,B1,C1的坐标(直接写答案)
A1(-1,2) B1(-3,1) C1(-2,-1)
(3)求△ABC各边的长.
分析 (1)作出各点关于y轴的对称点,再顺次连接即可;
(2)根据各点在坐标系中的位置写出各点坐标即可;
(3)利用勾股定理求出△ABC各边的长.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)由图可知,A1(-1,2),B1(-3,1),C1(-2,-1).
故答案为:(-1,2),(-3,1),(-2,-1);
(3)由勾股定理得,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$;
AC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$;BC=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$.
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
12.已知△ABC与△DEF的三边对应相等,三个角也对应相等,则能判定△ABC与△DEF全等的方法有( )种.
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
17.下列计算结果正确的是( )
| A. | $\sqrt{{{(-3)}^2}}=3$ | B. | $\sqrt{36}$=±6 | C. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | D. | $3+2\sqrt{3}=5\sqrt{3}$ |
14.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.给出下列说法:①抛物线的对称轴是直线x=1;②抛物线一定经过点(3,0);③在对称轴左侧,y随x增大而减小;④若A(-$\frac{3}{4}$,y1)、B($\frac{7}{5}$,y2)两点在此抛物线上,则y1>y2.上述说法正确的个数有( )
| x | … | -3 | -2 | -1 | 1 | 2 | … |
| y | … | -6 | 0 | 4 | 6 | 4 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.已知下列方程:①xy-1=2;②0.3x=4;③x=1;④x2-4x=3;⑤2x+3y=6,是一元一次方程的有( )个.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
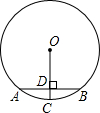 如图,AB为⊙O的弦,OC⊥AB于点D,交⊙O于点C.若⊙O的半径为5,AB=6,则CD的长是1.
如图,AB为⊙O的弦,OC⊥AB于点D,交⊙O于点C.若⊙O的半径为5,AB=6,则CD的长是1.
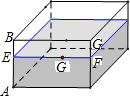 有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).
有一个如图示的长方体的透明玻璃杯,其长AD=7cm,高AB=5cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=4cm;一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物;小虫爬行的最短路线长为2$\sqrt{13}$cm(不计杯壁厚度).