题目内容
10．
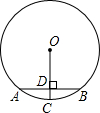如图，AB为⊙O的弦，OC⊥AB于点D，交⊙O于点C．若⊙O的半径为5，AB=6，则CD的长是1．
分析 连接OA，先利用垂径定理得出AD的长，再由勾股定理得出OD的长即可解答．
解答 
解：连接OA，
∵AB=6，OC⊥AB于点D，
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3，
∵⊙O的半径为5，
∴OD=$\sqrt{{OA}^{2}-{AD}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴CD=OC-OD=5-4=1．
故答案为：1
点评 本题考查的是垂径定理及勾股定理，解答此题的关键是作出辅助线构造出直角三角形，再利用勾股定理求解．
练习册系列答案
相关题目
18．下列计算正确的是（ ）
| A． | -（-2）=-2 | B． | $（{-3}）×（{-\frac{2}{3}}）=6$ | C． | -34=（-3）4 | D． | （-1）2=12 |
5．若实数a、b满足（a+b）（2a+2b-1）-1=0，则a+b=（ ）
| A． | 1 | B． | -$\frac{1}{2}$ | C． | 1或-$\frac{1}{2}$ | D． | 2 |
（1）如图，在平面直角坐标系中，A（1，2），B（3，1），C（-2，-1）．在图中作出△ABC关于y轴对称的△A1B1C1；
19．下列解方程过程中变形正确的是（ ）
| A． | 由3x-2=2x+1，移项得3x+2x=2+1 | |
| B． | 由$\frac{x-2}{2}$-$\frac{3x-2}{4}$=-1，去分母得2（x-2）-3x-2=-4 | |
| C． | 由2-3（x-1）=4，去括号得2-3x+3=4 | |
| D． | 由2x+3-x=5，合并同类项得3x+3=5． |
已知二次函数y=x2+mx+n的图象经过点P（-3，1），对称轴是经过（-1，0）且平行于y轴的直线．