题目内容
11．
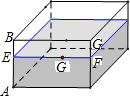有一个如图示的长方体的透明玻璃杯，其长AD=7cm，高AB=5cm，水深为AE=4cm，在水面线EF上紧贴内壁G处有一粒食物，且EG=4cm；一小虫想从杯外的A点沿壁爬进杯内G处吃掉食物；小虫爬行的最短路线长为2$\sqrt{13}$cm（不计杯壁厚度）．
分析 作出A关于BC的对称点A′，连接A′G，与BC交于点Q，此时AQ+QG最短，A′G为直角△A′EG的斜边，根据勾股定理求解即可．
解答 
解：如图所示，AQ+QG为最短路程．
∵在直角△AEG中，AE=4cm，AA′=10cm，
∴A′E=6cm，
又∵EG=4cm，
∴AQ+QG=A′Q+QG=A′G=$\sqrt{A′{E}^{2}+E{G}^{2}}$=2$\sqrt{13}$cm．
∴最短路线长为2$\sqrt{13}$cm．
故答案为：2$\sqrt{13}$．
点评 本题考查了轴对称-最短路径问题，熟知两点之间线段最短，是解答此题的关键．
练习册系列答案
相关题目
（1）如图，在平面直角坐标系中，A（1，2），B（3，1），C（-2，-1）．在图中作出△ABC关于y轴对称的△A1B1C1；
19．下列解方程过程中变形正确的是（ ）
| A． | 由3x-2=2x+1，移项得3x+2x=2+1 | |
| B． | 由$\frac{x-2}{2}$-$\frac{3x-2}{4}$=-1，去分母得2（x-2）-3x-2=-4 | |
| C． | 由2-3（x-1）=4，去括号得2-3x+3=4 | |
| D． | 由2x+3-x=5，合并同类项得3x+3=5． |
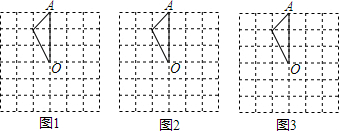
如图，二次函数y=ax2+bx+c图象的对称轴是x=$\frac{1}{3}$，下面四条信息：①abc＜0，②a+2b+4c＜0，③2a+3b=0，④2c＞5b．你认为其中正确的有（ ）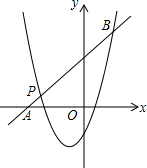
已知二次函数y=x2+mx+n的图象经过点P（-3，1），对称轴是经过（-1，0）且平行于y轴的直线．