题目内容
15.(1)计算:|1-$\sqrt{3}$|+3tan30°-(2017-π)0-(-$\frac{1}{3}$)-1.(2)已知x、y满足方程组$\left\{\begin{array}{l}{2x-y=1}\\{-x+2y=2}\end{array}\right.$,求代数式$\frac{1}{x-1}$•$\frac{{x}^{2}-1}{x+y}$-$\frac{x}{x+y}$的值.
分析 (1)根据绝对值、特殊角的三角函数值、零指数幂、负整数指数幂分别求出每一部分的值,再代入求出即可;
(2)先根据方程组求出x+y=3,算乘法,再算减法,最后代入求出即可.
解答 解:(1)原式=$\sqrt{3}$-1+3×$\frac{\sqrt{3}}{3}$-1-(-3)
=$\sqrt{3}$-1+$\sqrt{3}$-1+3
=2$\sqrt{3}$+1;
(2)∵方程组$\left\{\begin{array}{l}{2x-y=1}\\{-x+2y=2}\end{array}\right.$中的两个方程相加得:x+y=3,
∴$\frac{1}{x-1}$•$\frac{{x}^{2}-1}{x+y}$-$\frac{x}{x+y}$
=$\frac{1}{x-1}$•$\frac{(x+1)(x-1)}{x+y}$-$\frac{x}{x+y}$
=$\frac{x+1}{x+y}$-$\frac{x}{x+y}$
=$\frac{1}{x+y}$
=$\frac{1}{3}$.
点评 本题考查了绝对值、特殊角的三角函数值、零指数幂、负整数指数幂,解二元一次方程组,分式的混合运算和求值等知识点,能灵活运用知识点进行化简和计算是解此题的关键.

练习册系列答案
相关题目
4.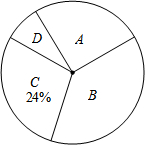 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
(1)表中的a=0.3b=6;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
 近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,
近期电视剧《人民的名义》热播,某校“话剧表演”社团在本校学生中开展学生知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“自己看过”,B类表示“听家长讲过”,C类表示“听同学讲过”,D类表示“不知道”,划分类别后的数据整理如表:
| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?
5.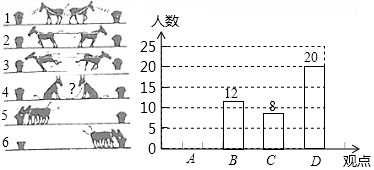 主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
A.放下自我,彼此尊重;
B.放下利益,彼此平衡;
C.放下性格,彼此成就;
D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
(1)参加本次讨论的学生共有50人;
(2)表中a=10,b=0.16;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
 主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:
主题班会课上,王老师出示了如图所示的一幅漫画,经过同学们的一番热议,达成以下四个观点:A.放下自我,彼此尊重;
B.放下利益,彼此平衡;
C.放下性格,彼此成就;
D.合理竞争,合作双赢.
要求每人选取其中一个观点写出自己的感悟,根据同学们的选择情况,小明绘制了如图两幅不完整的图表,请根据图表中提供的信息,解答下列问题:
| 观点 | 频数 | 频率 |
| A | a | 0.2 |
| B | 12 | 0.24 |
| C | 8 | b |
| D | 20 | 0.4 |
(2)表中a=10,b=0.16;
(3)将条形统计图补充完整;
(4)现准备从A,B,C,D四个观点中任选两个作为演讲主题,请用列表或画树状图的方法求选中观点D(合理竞争,合作双赢)的概率.
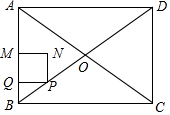 如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).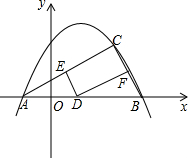 如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.
如图,已知抛物线y=-$\frac{1}{2}{x^2}$+bx+c图象经过A(-1,0),B(4,0)两点.