题目内容
5.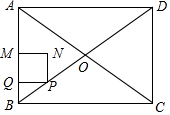 如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,矩形ABCD的对角线相交于点O,AB=6cm,BC=8cm,动点P以1cm/s的速度从点B出发,沿B→O→C向终点C运动,当点P在OB上运动时,过点P作PQ⊥AB于点Q,以PQ为边向上方作正方形PQMN,当点P在OC上运动时,过点P作PQ∥AB交OD于点Q,以PQ为边向左侧作正方形PQMN,设正方形PQMN与△ABO重叠部分图形的面积为S(cm2),点P运动的时间为t(s).(1)当点N在边AC上时,求t的值;
(2)当点P在OB上运动时,求S与t之间的函数关系式;
(3)当直线AN将矩形ABCD分成面积为1:3两部分时,直接写出t的值.
分析 (1)如图1中,当点N在边AC上时,易知PB=t,PQ=MN=$\frac{4}{5}$t,BQ=$\frac{3}{5}$t,由MN∥BC,推出$\frac{MN}{BC}$=$\frac{AM}{AB}$,列出方程即可解决问题;
(2)分三种情形讨论①如图2中,当0<t≤3时,重叠部分是正方形MNPQ.②如图3中,当3<t≤$\frac{30}{7}$时,重叠部分是五边形MQPEF.③如图4中,当$\frac{30}{7}$<t≤5时,重叠部分是四边形AQPE.分别求解即可;
(3)分三种情形①如图5中,当直线AN将矩形ABCD分成面积为1:3两部分时,易知BE=EC=4.②如图6中,当直线AN将矩形ABCD分成面积为1:3两部分时,易知DE=EC=3.③如图7中,当直线AN将矩形ABCD分成面积为1:3两部分时,易知BE=EC=4.俯角列出方程即可解决问题;
解答 解:(1)如图1中,当点N在边AC上时.
∵四边形ABCD是矩形,
∴AB=CD=6,BC=AD=8,∠BAD=90°,
∴BD=AC=10,cos∠ABO=cos∠BAO=$\frac{3}{5}$,
易知PB=t,PQ=MN=$\frac{4}{5}$t,BQ=$\frac{3}{5}$t,
∵MN∥BC,
∴$\frac{MN}{BC}$=$\frac{AM}{AB}$,
∴$\frac{\frac{4}{5}t}{8}$=$\frac{6-\frac{3}{5}t-\frac{4}{5}t}{6}$,
∴t=3.
(2)如图2中,当0<t≤3时,重叠部分是正方形MNPQ,S=($\frac{4}{5}$t)2=$\frac{16}{25}$t2.
如图3中,当3<t≤$\frac{30}{7}$时,重叠部分是五边形MQPEF,
S=S正方形MNPQ-S△PEN=$\frac{16}{25}$t2-$\frac{1}{2}$•[$\frac{4}{5}$t-$\frac{6}{5}$(5-t)]•$\frac{4}{3}$•[$\frac{4}{5}$t-$\frac{6}{5}$(5-t)]=-$\frac{152}{75}$t2+16t-24.
如图4中,当$\frac{30}{7}$<t≤5时,重叠部分是四边形AQPE,
S=$\frac{1}{2}$[$\frac{6}{5}$(5-t)+6-$\frac{3}{5}$t]•$\frac{4}{5}$t=-$\frac{18}{25}$t2+$\frac{24}{5}$t.
(3)如图5中,当直线AN将矩形ABCD分成面积为1:3两部分时,易知BE=EC=4,
∵MN∥BE,
∴$\frac{MN}{BE}$=$\frac{AM}{AB}$,
∴$\frac{\frac{4}{5}t}{4}$=$\frac{6-\frac{3}{5}t-\frac{4}{5}t}{6}$,
∴t=$\frac{30}{13}$.
如图6中,当直线AN将矩形ABCD分成面积为1:3两部分时,易知DE=EC=3,
∵tan∠ANM=tan∠DAE,
∴$\frac{AM}{NM}$=$\frac{ED}{AD}$,
∴$\frac{6-\frac{3}{5}t-\frac{4}{5}t}{\frac{4}{5}t}$=$\frac{3}{8}$,
∴t=$\frac{60}{17}$.
如图7中,当直线AN将矩形ABCD分成面积为1:3两部分时,易知BE=EC=4,
∵PN∥EC,
∴$\frac{PN}{EC}$=$\frac{AP}{AC}$,
∴$\frac{\frac{6}{5}(t-5)}{4}$=$\frac{5+t-5}{10}$,
∴t=$\frac{15}{2}$.
点评 本题考查四边形综合题、矩形的性质、平行线分线段成比例定理、多边形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案| A. |  | B. |  | C. |  | D. |  |
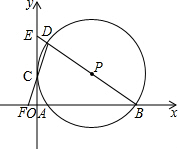 如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).
如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).