题目内容
7.(1)计算:($\sqrt{15}$-4)0+($\frac{1}{3}$)-1-2cos30°-|$\sqrt{3}$-2|(2)解不等式组:$\left\{\begin{array}{l}{3(2-x)≤x+5}\\{\frac{x+10}{3}>2x}\end{array}\right.$.
分析 (1)根据实数的混合运算顺序和法则计算可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原式=1+3-$\sqrt{3}$-2+$\sqrt{3}$=2;
(2)解不等式3(2-x)≤x+5,得:x≥$\frac{1}{4}$,
解不等式$\frac{x+10}{3}$>2x,得:x<2,
∴不等式组的解集为$\frac{1}{4}$≤x<2.
点评 本题考查的是实数的混合运算和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
16.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
| x | -1 | 0 | 1 | 3 |
| y | -3 | 1 | 3 | 1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.2的绝对值是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
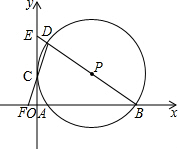 如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).
如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6). 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.