题目内容
8.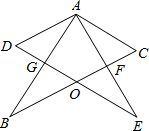 如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG=BG.其中正确的个数为( )
如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG=BG.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①根据已知得出∠CAF=30°,∠GAF=60°,进而得出∠AFB的度数;
②利用ASA证明△ADG≌△ACF得出答案;
③利用△AGO≌△AFO,得出AO=CO=AC,进而得出BO=CO=AO,即O为BC的中点;
④在Rt△AGE中,由∠AGE=90°,∠E=30°,推出AG=$\frac{1}{2}$AE,又AB=AE,可得AG=$\frac{1}{2}$AB解决问题.
解答 解:∵两块完全相同的含30°角的直角三角板叠放在一起,且∠DAB=30°.
∴∠CAF=30°,
∴∠GAF=60°,
∴∠AFB=90°,
∴AF丄BC正确,故①正确,
∵AD=AC,∠DAG=∠CAF,∠D=∠C=60°,
∴△ADG≌△ACF正确,故②正确,
∵△ADG≌△ACF,
∴AG=AF,
∵AO=AO,
∠AGO=∠AFO=90°,
∴△AGO≌△AFO,
∴∠OAF=30°,
∴∠OAC=60°,
∴AO=CO=AC,
∴BO=CO=AO,故③正确,
在Rt△AGE中,∵∠AGE=90°,∠E=30°,
∴AG=$\frac{1}{2}$AE,
∵AB=AE,
∴AG=$\frac{1}{2}$AB,
∴AG=GB,故④正确.
故选D.
点评 此题主要考查了全等三角形的判定和性质、直角三角形中30度角的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.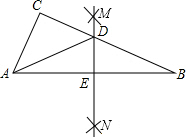 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧交于点M、N,过点M、N作直线交BC于点D,交AB于点E,连接AD.若△ABC的周长为16,△ACD的周长为9,那么线段AE的长是( )| A. | 3.5 | B. | 5 | C. | 7 | D. | 8 |
19.若二次函数y=x2+bx+c的图象与x轴交于两点,与y轴的正半轴交于一点,且对称轴为x=1,则下列说法正确的是( )
| A. | 二次函数的图象与x轴的交点位于y轴的两侧 | |
| B. | 二次函数的图象与x轴的交点位于y轴的右侧 | |
| C. | 其中二次函数中的c>1 | |
| D. | 二次函数的图象与x轴的一个交于位于x=2的右侧 |
16.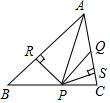 如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
 如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )
如图,已知△ABC中,AQ=PQ、PR=PS、PR⊥AB于R,PS⊥AC于S,有以下三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,其中( )| A. | 全部正确 | B. | 仅①正确 | C. | 仅①、②正确 | D. | 仅①、③正确 |
13. 以图中方格纸的3个格点为顶点画出三角形,不全等的三角形有( )种.
以图中方格纸的3个格点为顶点画出三角形,不全等的三角形有( )种.
 以图中方格纸的3个格点为顶点画出三角形,不全等的三角形有( )种.
以图中方格纸的3个格点为顶点画出三角形,不全等的三角形有( )种.| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
20.已知三角形的两边长分别为4和6,则第三边的中线长x的取值范围是( )
| A. | 1<x<5 | B. | 2<x<10 | C. | 4<x<20 | D. | 无法确定 |
17.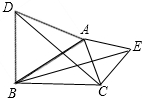 已知:如图,△ABD和△ACE均为等腰三角形,且∠DAB=∠CAE=60°,则△ADC≌△AEB的根据是( )
已知:如图,△ABD和△ACE均为等腰三角形,且∠DAB=∠CAE=60°,则△ADC≌△AEB的根据是( )
 已知:如图,△ABD和△ACE均为等腰三角形,且∠DAB=∠CAE=60°,则△ADC≌△AEB的根据是( )
已知:如图,△ABD和△ACE均为等腰三角形,且∠DAB=∠CAE=60°,则△ADC≌△AEB的根据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
18.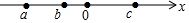 实数a,b,c在数轴上对应的点如图,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图,则下列式子中正确的是( )
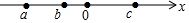 实数a,b,c在数轴上对应的点如图,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图,则下列式子中正确的是( )| A. | a-c>b-c | B. | ac>bc | C. | a+c<b+c | D. | $\frac{a}{b}$<$\frac{c}{b}$ |