题目内容
17.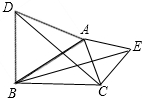 已知:如图,△ABD和△ACE均为等腰三角形,且∠DAB=∠CAE=60°,则△ADC≌△AEB的根据是( )
已知:如图,△ABD和△ACE均为等腰三角形,且∠DAB=∠CAE=60°,则△ADC≌△AEB的根据是( )| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
分析 根据等腰三角形得出AD=AB,AE=AC,求出∠DAC=∠EAB,根据全等三角形的判定推出即可.
解答 解:∵△ABD和△ACE均为等腰三角形,
∴AD=AB,AE=AC,
∵∠DAB=∠CAE=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠EAB,
在△ADC和△AEB中
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$
∴△ADC≌△AEB(SAS),
故选B.
点评 本题考查了全等三角形的判定定理和等腰三角形的性质,能熟记全等三角形的判定定理内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.2016年6月13日,保定市首届中学生校园足球比赛在保定一中开幕,参加比赛的共有23支代表队,其中初中男生队有8(A-H)支代表队,若从这8支代表队中随机抽取两支进行一场比赛,则恰好抽到A代表队和C代表队的概率是( )
| A. | $\frac{1}{28}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{56}$ | D. | $\frac{1}{64}$ |
2. 如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
 如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )| A. | 130° | B. | 65° | C. | 35° | D. | 25° |
9.下面四个图形中,既是轴对称又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.若|x+3|+|y-2|=0,则x+y的值为( )
| A. | 5 | B. | -5 | C. | -1 | D. | 1 |
7.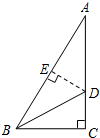 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若CD=3cm,则点D到AB的距离DE是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
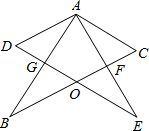 如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG=BG.其中正确的个数为( )
如图所示,两个完全相同的含30°角的Rt△ABC和Rt△AED叠放在一起,BC交DE于点O,AB交DE于点G,BC交AE于点F,且∠DAB=30°,以下三个结论:①AF⊥BC;②△ADG≌△ACF;③O为BC的中点;④AG=BG.其中正确的个数为( ) 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,动点P从D点开始沿DA以2cm/s的速度向A运动,动点Q从B点开始沿BC以1cm/s的速度向C运动,P、Q分别从D、B同时出发,当其中一点到端点时,另一点也随之停止运动,连结PQ,设运动时间为t.
如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=3cm,BC=20cm,动点P从D点开始沿DA以2cm/s的速度向A运动,动点Q从B点开始沿BC以1cm/s的速度向C运动,P、Q分别从D、B同时出发,当其中一点到端点时,另一点也随之停止运动,连结PQ,设运动时间为t.