题目内容
20.如图,把带有指针的圆形转盘A、B分别分成4等份、3等份的扇形区域,并在每一个小区域内标上数字(如图所示).小明、小乐两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为3的倍数,则小明胜;否则,小乐胜.(若有指针落在分割线上,则无效,需重新转动转盘)(1)试用列表或画树状图的方法,求小明获胜的概率;
(2)请问这个游戏规则对小明、小乐双方公平吗?做出判断并说明理由.

分析 (1)列举出所有情况,看指针所指两区域的数字之积为3的倍数的情况占总情况的多少,即可求得小明胜的概率;
(2)由(1)进而求得小乐胜的概率,比较两个概率即可得出游戏是否公平.
解答 解:(1)根据题意画图如下:
共有12种情况,指针所指两区域的数字之积为3的倍数的有6种情况,则小明胜的概率是$\frac{6}{12}$=$\frac{1}{2}$;
(2)由(1)得小乐胜的概率为1-$\frac{1}{2}$=$\frac{1}{2}$,两人获胜的概率相同,所以游戏公平.
点评 此题考查了概率的公平性,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$,注意本题是放回实验.解决本题的关键是得到相应的概率,概率相等就公平,否则就不公平.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.分式方程$\frac{x}{{x}^{2}-4}$+$\frac{2}{x+2}$=$\frac{1}{x-2}$的根是( )
| A. | x=1 | B. | x=-1 | C. | x=3 | D. | x=-3 |
8.下列事件中,为必然事件是( )
| A. | 度量三角形的内角和,结果是360° | |
| B. | 从仅装有5个黑球的口袋中摸出一球是黑球 | |
| C. | 购买中奖率为1%的100张彩票,结果中奖 | |
| D. | 汽车累积行驶1万千米,从未出现故障 |
15. 如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
 如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )
如图,A、D是电线杆AB上的两个瓷壶,AC和DE分别表示太阳光线,若某一时刻线段AD在地面上的影长CE=1m,BD在地面上的影长BE=3m,瓷壶D到地面的距离DB=20m,则电线杆AB的高为( )| A. | 15m | B. | $\frac{80}{3}$m | C. | 21m | D. | $\frac{60}{7}$m |
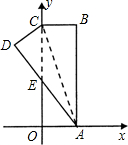 如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.若双曲线$y=\frac{k}{x}$经过点D,则k=-$\frac{48}{25}$.
如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.若双曲线$y=\frac{k}{x}$经过点D,则k=-$\frac{48}{25}$.